Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями

Настоящая задача о блуждании весьма популярна и имеет много формулировок. Далее мы будем трактовать ее как задачу о частице, движущейся по оси.

Рассмотрим частицу, которая сначала находится в положении x = 1 на оси. Структура задачи будет яснее, если вероятность шага направо вместо 2/3 будет равна p . Частица движется из положения 1 либо в точку x = 2 с вероятностью p , либо в точку x = 0 с вероятностью 1 − p (рис. 7). Вообще, если частица находится в положении x = n , n > 0, n — целое число, то она сдвигается либо в точку x = n + 1 с вероятностью p , либо в точку x = n − 1 с вероятностью 1 − p . Если частица попадает в положение x = 0, то там она поглощается (не делает других шагов). Нас интересует значение вероятности P ₁ того, что частица поглощается в точке x = 0, если она выходит из точки x = 1. Разумеется, значение P ₁ зависит от p . Кажется естественным, что если p близко к 1, то вероятность P ₁ мала, а если p близко к нулю, то P ₁ мало отличается от 1.

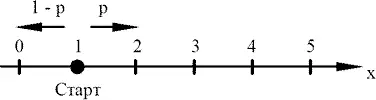
Рис. 7.

Рассмотрим ситуацию после первого шага: либо частица сдвинулась налево, попала в точку x = 0 и поглотилась там (это событие имеет вероятность 1 − p ), либо сдвинулась направо в точку x = 2 (это событие происходит с вероятностью p ). Пусть P ₂ обозначает вероятность того, что частица поглощается в начале координат x = 0, если она выходит из точки x = 2. Тогда мы имеем

P ₁ = 1 − p + p · P ₂, (1)

так как 1 − p есть вероятность поглощения на первом шаге и p · P ₂ — вероятность поглощения на последующих шагах.

Каждый путь, ведущий к поглощению из x = 2, можно разбить на две части:

(1) Путь, идущий из точки x = 2 и достигающий положения x = 1 в первый раз (не обязательно за один шаг) и

(2) Путь, идущий из точки x = 1 в точку x = 0 (также не обязательно за один шаг). Вероятность пути из положения x = 2 в x = 1 есть P ₁ поскольку структура блуждания здесь идентична структуре первоначального блуждания (см. рис. 35.1), за исключением того, что начало координат переносится на один шаг направо. Вероятность попасть из точки x = 1 в x = 0 также равна P ₁ как и в исходной задаче. Величина P ₂ поэтому есть P ₁², так как события A (частица идет по пути от точки x = 2 к x = 1) и B (частица движется по пути от точки x = 1 до x = 0) независимы, и P ( A ) = P ( B ) = P ₁.

Мы можем переписать уравнение (1) как

P ₁ = 1 − p + p · P ₁², (2)

Уравнение (2) — квадратное относительно P ₁ и имеет два решения:

P ₁ = 1; P ₁ = (1 − p )/ p . (3)

В таких задачах одно или оба решения могут быть подходящими, в зависимости от значений p .

Если p = 1/2, то оба решения совпадают, и P ₁ = 1. Когда p = 1, P ₁ = 0, так как частица всегда движется вправо. И когда p = 0, очевидно, P ₁ = 1. При p < 1/2 второе решение (3) не подходит, так как тогда (1 − p )/p > 1, а по смыслу задачи P ₁ ≤ 1. Поэтому при 0 ≤ p ≤ 1/2 мы имеем P ₁ = 1.

Чтобы доказать, что второе решение P ₁ = (1 − p )/ p имеет место при p > 1/2, нам достаточно установить, что P ₁ является непрерывной функцией от p (грубо говоря, что P ₁ не слишком изменяется, когда p меняется мало). Мы предполагаем эту непрерывность, но не доказываем ее.

Кривая (см. рис. 8) начинается в точке P ₁ = 1 при p = 1/2; она должна спуститься к P = 0 при p = 1, и ее ордината всегда должна равняться 1 или (1 − p )/ p . Кривая не имеет разрывов только в том случае, когда при p > 1/2 соответствующее значение равно (1 − p )/ p . Итак, при предположении непрерывности функции P ₁ мы получаем P ₁ = (1 − p )/ p при p > 1/2. Поэтому наш пьяница с вероятностью 1/2 упадет вниз.

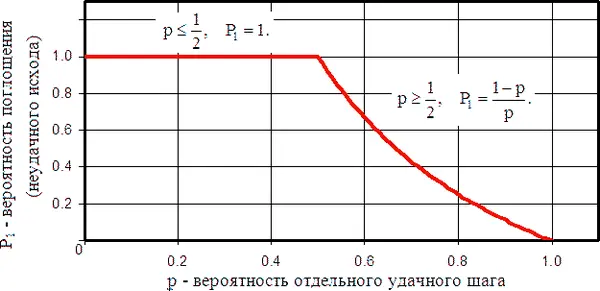
Рис. 8. Вероятности поглощения P .

Приведем другую интерпретацию. Рассмотрим игрока, имеющего начальный капитал в одну денежную единицу ( x = 1). Он может играть неограниченно долго, причем в каждом туре игры он с какими-то вероятностями выигрывает или проигрывает эту единицу. Чтобы вероятность банкротства игрока была не более 1/2, вероятность выигрыша в отдельной партии должна быть не менее 2/3. То, что банкротство неизбежно при p = 1/2, для большинства из нас неожиданность.