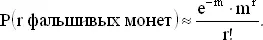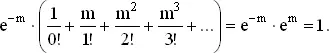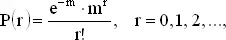Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями
Здесь есть возможность читать онлайн «Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями» весь текст электронной книги совершенно бесплатно (целиком полную версию без сокращений). В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: Математика, на русском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Пятьдесят занимательных вероятностных задач с решениями
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4.5 / 5. Голосов: 2
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Пятьдесят занимательных вероятностных задач с решениями: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Пятьдесят занимательных вероятностных задач с решениями»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Книга обращена к широкому кругу читателей: ученикам старших классов, педагогам, студентам.

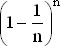 , получим следующее выражение:
, получим следующее выражение: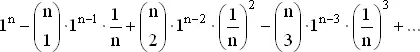
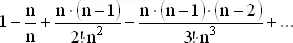 (1)
(1)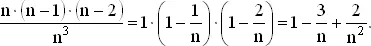 (2)
(2)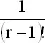
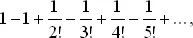
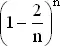 , сходилась бы при больших n к e −2и, точно так же,
, сходилась бы при больших n к e −2и, точно так же, 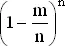 стремится к e −m . Вообще
стремится к e −m . Вообще 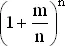 стремится к e m при любом (целом или нет) значении m . Эти факты будут использованы в дальнейшем. Более строгое их обоснование можно найти в любом учебнике по дифференциальному исчислению.
стремится к e m при любом (целом или нет) значении m . Эти факты будут использованы в дальнейшем. Более строгое их обоснование можно найти в любом учебнике по дифференциальному исчислению.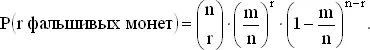
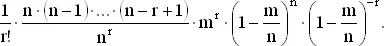
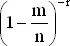 стремится к 1 (так как m и r фиксированы). Поэтому при больших n
стремится к 1 (так как m и r фиксированы). Поэтому при больших n