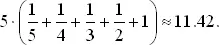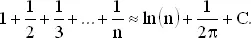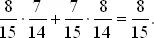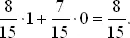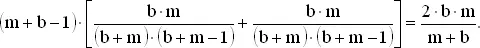1) A и B освобождаются, и охранник говорит B , вероятность 1/3.
2) A и C освобождаются, и охранник говорит C , вероятность 1/3.
3) B и C освобождаются, и охранник говорит B , вероятность 1/6.
4) B и C освобождаются, и охранник говорит C , вероятность 1/6.
Если на вопрос A охранник отвечает B , то апостериорная вероятность освобождения А равна вероятности исхода 1, деленной на сумму вероятностей исходов 1 и 3. Таким образом, вероятность освобождения A равна (1/3)/(1/3 + 1/6) = 2/3, так что математический расчет в конце концов отвечает здравому смыслу.
14. Решение задачи о выборе купонов
Из первой коробки мы достаем один купон. Далее, вероятность получить новый номер из второй коробки равна 4/5. Используя ответ задачи 4, видим, что приобретение нового номера потребует в среднем (4/5) −1= 5/4 коробок. Третий номер потребует (3/5) −1= 5/3, четвертый 5/2, пятый — 5 коробок.
Таким образом, среднее число коробок равно
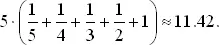
Формула Эйлера для сумм гармонического ряда
Хотя в данном случае указанные дроби сложить, но когда в комплекте большое число купонов, удобно применить формулу Эйлера для частичных сумм гармонического ряда:
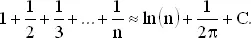
(Число C = 0.57721... называется постоянной Эйлера.) В случае комплекта из n купонов среднее число коробок приближенно равно
n ·log n + 0.577 n + ½.
Поскольку log 5 ≈ 1.6094, формула Эйлера при n = 5 дает 11.43, что весьма близко к 11.42. Членом 1/2 n в формуле Эйлера часто пренебрегают.
15. Решение задачи о театре
Например, если ряд заполнен следующим образом
BBMMBBMBMBMBBMM
(здесь B обозначает юношу, а M — девушку), то имеется 9 пар BM и MB .
Нас интересует среднее число таких пар. Если первые два места в ряду заняты лицами разных полов, то у нас уже имеется искомая пара. Вероятность этого события равна
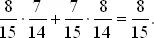
Более того, 8/15 есть и среднее число пар на первых двух местах, так как
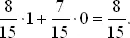
Такое же рассуждение применимо к каждой паре смежных мест.
Для определения среднего числа пар молодых людей эту величину надо умножить на число смежных мест, равное 14, что дает 112/15.
Более общим образом, если есть b объектов одного рода и m другого, располагаемых случайным образом в ряд, то среднее число пар, составленных из различных объектов, равно
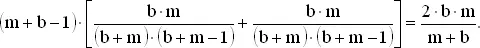
В нашем примере b = 8, m = 7, и ответ равен 112/15.
Здесь мы существенным образом использовали тот факт, что математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых. Мы нашли среднее число пар BM или MB для каждых двух смежных мест и просуммировали по всем таким двойкам.
16. Рещение задачи о распределении призовых мест
Ответ равен 4/7. Второй по мастерству игрок может занять второе место лишь в том случае, когда он находится в половине турнирной лестницы, не занимаемой лучшим игроком.
Если в турнире участвуют 2 n игроков, то в половине турнирной лестницы, не занимаемой лучшим игроком, 2 n − 1начальных ступеней, а всего имеется 2 n − 1 начальных ступеней (кроме занятой лучшим игроком). Таким образом, в турнире с 2 n игроками второй по мастерству может с вероятностью 2 n − 1/(2 n − 1) занять второе место.
17. Решение задачи о рыцарях-близнецах
(а). Обозначим близнецов через A к B . Пусть A занимает высшую ступень турнирной лестницы. Если B занимает смежное место, что происходит с вероятностью 1/7, то они заведомо встретятся в первом туре. Вероятность того, что B находится в паре, соседней с парой A , равна 4/7, и вероятность того, что они встретятся в этом случае, равна 1/7, так как для осуществления этого события каждый должен победить в первом поединке. Наконец, вероятность того, что B находится в нижней половине, равна 4/7, и в этом случае вероятность встречи равна 1/2 4= 1/16, так как оба должны выиграть в двух турах. Таким образом, полная вероятность встречи равна
Читать дальше