A.A. Lokshin - Аннотация

В этом параграфе приводится геометрическая иллюстрация (также являющаяся одновременно доказательством) другого известного комбинаторного закона – рекуррентного соотношения для числа сочетаний из n элементов по k элементов ():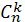

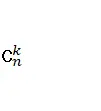(1)

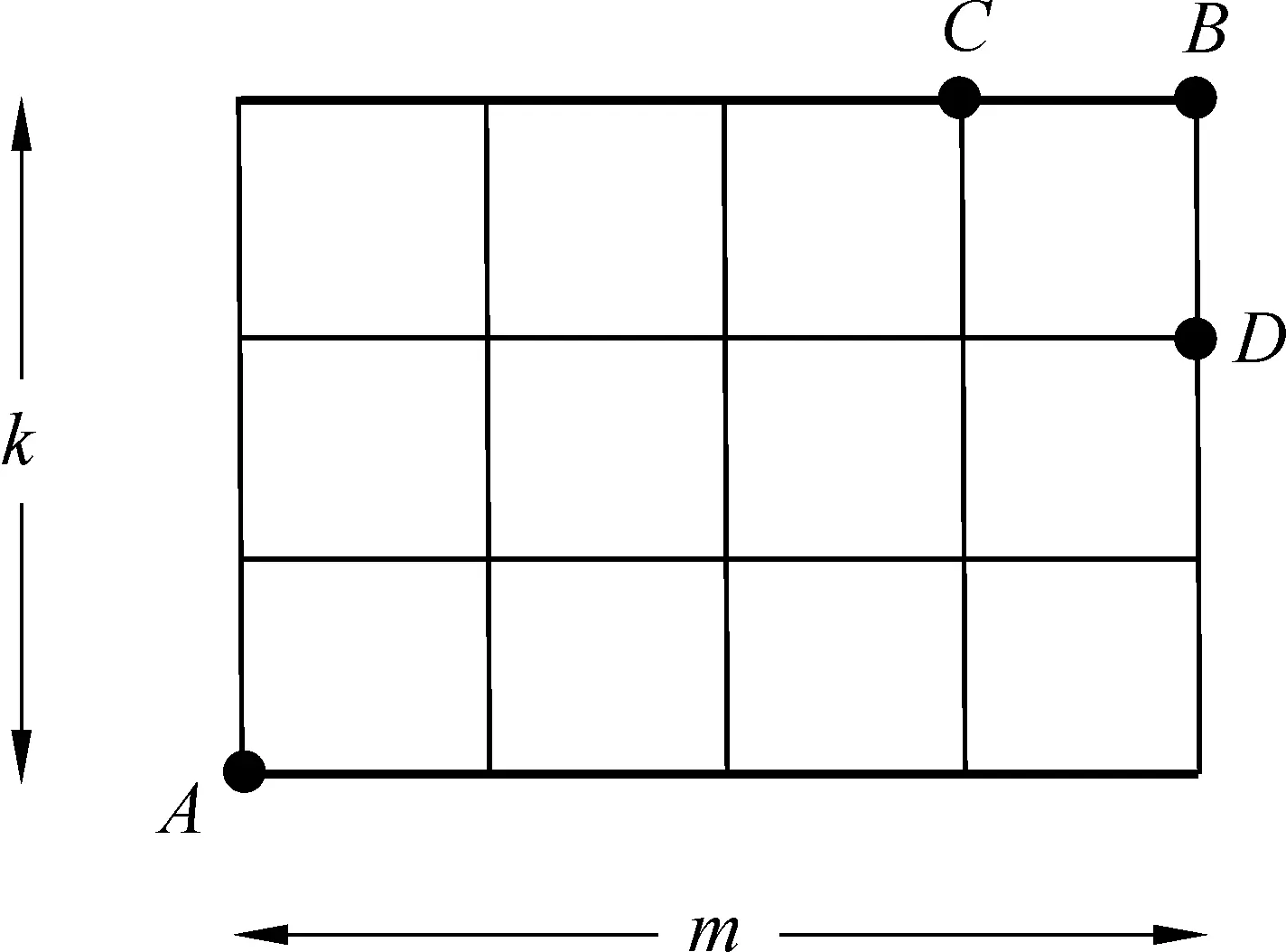
Рассмотрим прямоугольник размера m × k , составленный из единичных квадратов (см. рис. 7.1). Нас будет интересовать число маршрутов из нижнего левого угла A в правый верхний угол B ( двигаться можно только вверх или вправо по сторонам едини ч ных квадратов ). Это число мы обозначим через N ( m, k ).

Заметим теперь, что попасть в точку B можно только одним из двух способов: либо из точки C , либо из точки D , cледовательно,

N ( m,k ) = N ( m –1 ,k) + N ( m,k –1) (2)

(справедливость этого соотношения геометрически очевидна; при этом существенно то обстоятельство, что двигаться из точки A можно только либо вверх, либо вправо).

Покажем теперь, что геометрически очевидное соотношение (2) это и есть, в сущности, другая (причем более симметричная!) форма записи комбинаторного равенства (1).

Действительно, длина любого маршрута из A в B равна в точности m + k . Пронумеруем теперь шаги произвольно взятого маршрута. Очевидно, что каждый маршрут полностью характеризуется номерами шагов, направленных вверх (этих шагов всего должно быть k штук). Тем самым каждый маршрут однозначно соответствует выбору k чисел из множества{1,2,…, m + k }.

Следовательно,

и мы можем переписать (2) в виде

Полагая здесь n = m + k , приходим к искомому равенству (1).

Объясняя студентам – будущим педагогам начальных классов – начала комбинаторики, неизбежно приходится вводить функцию n ! («эн-факториал»). С педагогической точки зрения здесь имеется одно довольно узкое место.

Мы полагаем по определению, что

n ! = n ( n –1)( n –2)·…·2 ·1 при n ≥ 1, (1)

а при n = 1 считаем опять же по определению, что

0! = 1. (2)

Соотношение (1) обычно не вызывает никаких затруднений – здесь все ясно: мы имеем дело с произведением всех натуральных чисел от n до 1. Но откуда берется соотношение (2)? Если не дать разумного, адекватного объяснения, четко указав то место, где действительно используется соглашение (2), то весь материал, связанный с биномиальными коэффициентами, будет воспринят отчасти на веру.

И тут у преподавателя, знакомого, естественно, с Гамма-функцией Эйлера, появляется искушение объяснить происхождение формулы (2) следующим образом.

При n > 1, очевидно, имеем

n ! = ( n –1)! · n . (3)

Мы хотим сохранить это же самое соотношение при n = 1. Подставляя в (3) n = 1, получаем

1! = 0!·1, (4)

откуда и следует (2).

Однако соотношение (4) нигде в курсе комбинаторики не

используется, и в результате остается непонятным, нельзя ли было положить 0! равным какому-нибудь другому числу, отличному от 1.

Выход из положения здесь, на наш взгляд, такой. Соображения (3), (4) можно (но не обязательно) рассказывать студентам в качестве дополнительного материала, но не стоит давать их непосредственно после формулы (2) для ее «оправдания».

Вместо этого, чтобы оправдать соглашение (2), на наш взгляд, следует сказать, что для того чтобы формулы, которые вскоре появятся, имели единообразный вид при всех n ≥ 0 (а не только при n ≥ 1) нужно, чтобы выражение

(5)

равнялось 1. (Действительно, как известно, каждое выражение вида при 0 < k < n представляет собой число сочетаний из n элементов по k элементов, т.е. число способов выбрать какие-нибудь k элементов из n данных элементов. При k = 0, очевидно, существует только один такой способ – не брать ни одного элемента.)

Поэтому неизбежно принятие соглашения (2). В результате, мы избегаем неприятного порочного круга в задаче: «Сколькими способами можно выбрать 0 элементов из n элементов?»

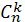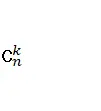(Имеется в виду следующий порочный круг: «Число этих способов равно числу сочетаний из n элементов по 0 элементов, т.е. равно выражению (5). Подставляя в (5) о п ределение (2) для 0!, получаем в ответе 1» ).