Выбор такой пары, очевидно, полностью определяет сам маршрут из А в В , и общее количество маршрутов из А в В вычисляется по правилу произведения и равно 2∙3 = 6. Число маршрутов из В в А тем самым также равно шести.
Возможны еще более любопытные конфигурации дорог между А и В , к которым по-прежнему применимо правило произведения для подсчета числа возможных маршрутов из А в В (и, соответственно, из В в А ). Пример такой конфигурации приведен на рис. 6.5.
Рис. 6.5
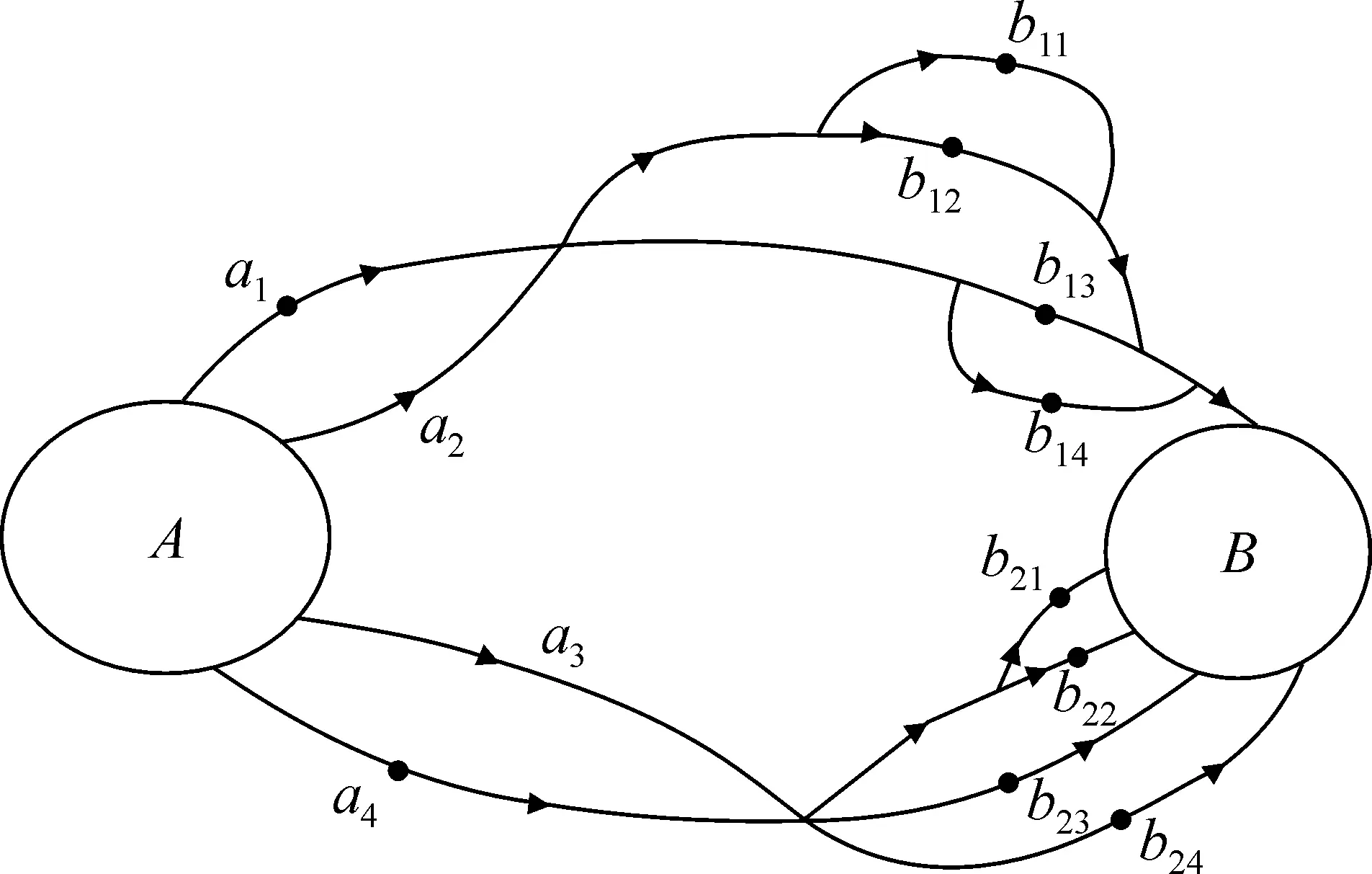
В ситуации, изображенной на рис. 6.5, маршрут из А в В лучше всего задавать упорядоченной парой точек вида ( a , b ), которую удается подобрать так, что она однозначно определяет выбранный маршрут. Нетрудно видеть, что после того как выбрана первая точка упорядоченной пары (т.е. выбрана точка a 1, a 2, 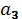 a 3 или a 4) выбор второй точки осуществляется одним из четырех способов. Поэтому в полном соответствии с правилом произведения число различных маршрутов из А в В на рис. 6.5 равно 4∙4 = 16.
a 3 или a 4) выбор второй точки осуществляется одним из четырех способов. Поэтому в полном соответствии с правилом произведения число различных маршрутов из А в В на рис. 6.5 равно 4∙4 = 16.
Рассмотрим еще один пример, когда маршрут из А в В определяется выбором упорядоченной тройки точек вида ( a, b, c ), расположенных на сети дорог (см. рис. 6.6).
Рис. 6.6
Первая координата упомянутой упорядоченной тройки точек может быть выбрана двумя способами ( a 1 или a 2). После того как этот выбор сделан вторая координата рассматриваемой упорядоченной тройки точек может быть выбрана тремя способами ( b 1 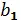 , b 2
, b 2 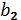 или b 3
или b 3 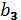 ). Наконец, после того как выбраны первая и вторая координаты упорядоченной тройки ( a, b, c ), третья координата тоже может быть выбрана одним из трех способов. Итак, по правилу произведения, число маршрутов из А в В на рис. 6.6 равно 2∙3∙3 =18.
). Наконец, после того как выбраны первая и вторая координаты упорядоченной тройки ( a, b, c ), третья координата тоже может быть выбрана одним из трех способов. Итак, по правилу произведения, число маршрутов из А в В на рис. 6.6 равно 2∙3∙3 =18.
Удобно ввести символ П 3  ( А , В ) для характеристики маршрутов, связывающих «города» А и В на рис. 6.6. Здесь буква Π указывает на то, что общее число маршрутов при движ е нии из А в В может быть вычислено с помощью правила произведения, индекс «3» указывает на (минимальное) количество точек, с помощью которых мы однозначно задаем маршрут.
( А , В ) для характеристики маршрутов, связывающих «города» А и В на рис. 6.6. Здесь буква Π указывает на то, что общее число маршрутов при движ е нии из А в В может быть вычислено с помощью правила произведения, индекс «3» указывает на (минимальное) количество точек, с помощью которых мы однозначно задаем маршрут.
Предположим теперь, что города А и В связывают две непересекающиеся системы дорог, относящиеся, например, к классам 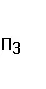 П3( А , В ) и П2( В , А ) соответственно. Тогда количество маршрутов из А в В , относящихся к первой системе, согласно правилу произведения вычисляется по формуле k∙m∙n , где k, m, n – количества способов выбрать первую, вторую и третью точки, задающие каждый маршрут из А в В . Аналогично, количество маршрутов второй системы вычисляется по формуле k ∙m , где k и m – количества способов выбрать соответственно первую и вторую точки, задающие маршруты второй системы (при движении из В в А ). Поскольку число маршрутов, принадлежащих любой системе, в конечном итоге не зависит от того, а какую сторону направлено движение, заключаем, что в нашей задаче общее число маршрутов из А в В (и тем самым из В в А ) будет равно k∙m∙n + k ∙m .
П3( А , В ) и П2( В , А ) соответственно. Тогда количество маршрутов из А в В , относящихся к первой системе, согласно правилу произведения вычисляется по формуле k∙m∙n , где k, m, n – количества способов выбрать первую, вторую и третью точки, задающие каждый маршрут из А в В . Аналогично, количество маршрутов второй системы вычисляется по формуле k ∙m , где k и m – количества способов выбрать соответственно первую и вторую точки, задающие маршруты второй системы (при движении из В в А ). Поскольку число маршрутов, принадлежащих любой системе, в конечном итоге не зависит от того, а какую сторону направлено движение, заключаем, что в нашей задаче общее число маршрутов из А в В (и тем самым из В в А ) будет равно k∙m∙n + k ∙m .
(Заметим, что прямой подсчет числа маршрутов в задачах такого рода может быть весьма трудоемким делом.)
Дальнейшие обобщения предложенного подхода очевидны: рассмотренные системы маршрутов типа П k ( А , В ) можно использовать как «строительные блоки» для конструирования более сложных систем.
Замечание.В дальнейшем мы увидим, что правило произведения может успешно применяться в задачах совершенно иного сорта.
7. ОБ ОДНОМ КОМБИНАТОРНОМ
СООТНОШЕНИИ
Опыт преподавания комбинаторики говорит о том, что наглядные геометрические соображения (если, конечно, ими удается воспользоваться) значительно облегчают усвоение материала. Например, важнейший закон комбинаторики – правило произведения – обычно иллюстрируют при помощи «деревьев» [5] См. предыдущий параграф.
. Эта же иллюстрация служит заодно вполне надежным доказательством упомянутого правила.
Читать дальше

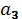 a 3 или a 4) выбор второй точки осуществляется одним из четырех способов. Поэтому в полном соответствии с правилом произведения число различных маршрутов из А в В на рис. 6.5 равно 4∙4 = 16.
a 3 или a 4) выбор второй точки осуществляется одним из четырех способов. Поэтому в полном соответствии с правилом произведения число различных маршрутов из А в В на рис. 6.5 равно 4∙4 = 16.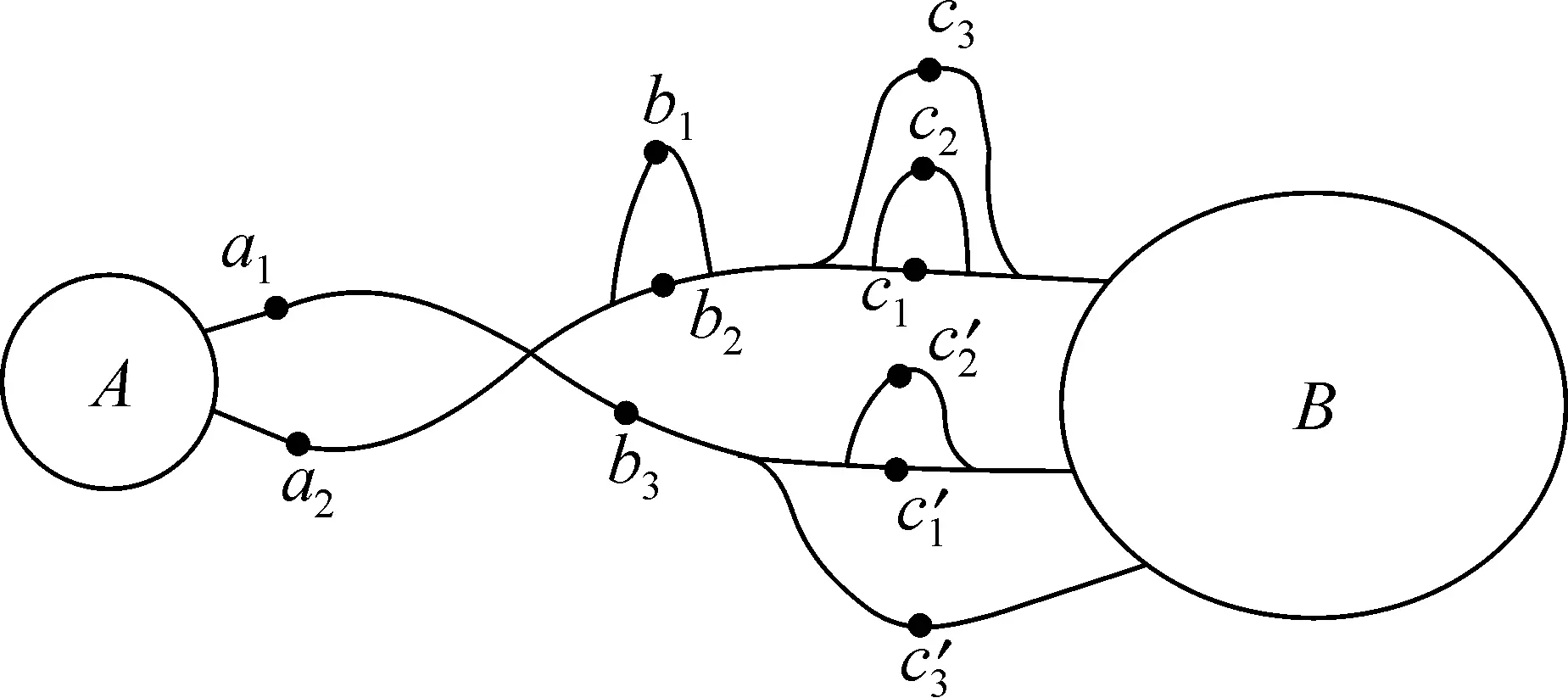
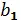 , b 2
, b 2 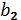 или b 3
или b 3 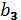 ). Наконец, после того как выбраны первая и вторая координаты упорядоченной тройки ( a, b, c ), третья координата тоже может быть выбрана одним из трех способов. Итак, по правилу произведения, число маршрутов из А в В на рис. 6.6 равно 2∙3∙3 =18.
). Наконец, после того как выбраны первая и вторая координаты упорядоченной тройки ( a, b, c ), третья координата тоже может быть выбрана одним из трех способов. Итак, по правилу произведения, число маршрутов из А в В на рис. 6.6 равно 2∙3∙3 =18. ( А , В ) для характеристики маршрутов, связывающих «города» А и В на рис. 6.6. Здесь буква Π указывает на то, что общее число маршрутов при движ е нии из А в В может быть вычислено с помощью правила произведения, индекс «3» указывает на (минимальное) количество точек, с помощью которых мы однозначно задаем маршрут.
( А , В ) для характеристики маршрутов, связывающих «города» А и В на рис. 6.6. Здесь буква Π указывает на то, что общее число маршрутов при движ е нии из А в В может быть вычислено с помощью правила произведения, индекс «3» указывает на (минимальное) количество точек, с помощью которых мы однозначно задаем маршрут.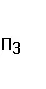 П3( А , В ) и П2( В , А ) соответственно. Тогда количество маршрутов из А в В , относящихся к первой системе, согласно правилу произведения вычисляется по формуле k∙m∙n , где k, m, n – количества способов выбрать первую, вторую и третью точки, задающие каждый маршрут из А в В . Аналогично, количество маршрутов второй системы вычисляется по формуле k ∙m , где k и m – количества способов выбрать соответственно первую и вторую точки, задающие маршруты второй системы (при движении из В в А ). Поскольку число маршрутов, принадлежащих любой системе, в конечном итоге не зависит от того, а какую сторону направлено движение, заключаем, что в нашей задаче общее число маршрутов из А в В (и тем самым из В в А ) будет равно k∙m∙n + k ∙m .
П3( А , В ) и П2( В , А ) соответственно. Тогда количество маршрутов из А в В , относящихся к первой системе, согласно правилу произведения вычисляется по формуле k∙m∙n , где k, m, n – количества способов выбрать первую, вторую и третью точки, задающие каждый маршрут из А в В . Аналогично, количество маршрутов второй системы вычисляется по формуле k ∙m , где k и m – количества способов выбрать соответственно первую и вторую точки, задающие маршруты второй системы (при движении из В в А ). Поскольку число маршрутов, принадлежащих любой системе, в конечном итоге не зависит от того, а какую сторону направлено движение, заключаем, что в нашей задаче общее число маршрутов из А в В (и тем самым из В в А ) будет равно k∙m∙n + k ∙m .