а) Как это удалось сделать Змею Горынычу?
б) Сколькими различными способами мог осуществить Змей Горыныч свою затею?
Решение.а) На первый взгляд, задача кажется трудной. Однако решение ее очнь простое. Нужно перенумеровать числами от 1 до N все города Карабасии и установить дорожные указатели так, чтобы каждая стрелка указывала направление от города с меньшим номером к городу с большим номером. Тогда, выехав из произвольно взятого города, в него будет невозможно вернуться. (При этом из города с номером N невозможно будет выехать.)
б) Ответ: N !
Задача 2.Верно ли, что если из каждого города в Карабасии можно выехать, то найдется хотя бы один город, в который можно будет вернуться? (Движение по всем дорогам Карабасии одностороннее.)
СПИСОК ОБОЗНАЧЕНИЙ
– квантор общности ( х – «для всех х»);
– квантор существования ( х – «найдется х »);
– дизъюнкция высказываний (А В – «А или В», в смысле «хотя бы одно из двух»);
– конъюнкция высказываний (А В – «А и В»);
¬– отрицание высказывания ( ¬А – «не А», «неверно, что А»);
– импликация высказываний (АВ – «если А, то В»);
– эквиваленция высказываний (АВ – «А тогда и только тогда, когда В»);
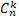 – число сочетаний из n элементов по k элементов, т.е. число различных k - элементных подмножеств n - элементного множества;
– число сочетаний из n элементов по k элементов, т.е. число различных k - элементных подмножеств n - элементного множества;
ЛИТЕРАТУРА
1. Иванова Е.А., Локшин А.А. О парадоксе математической индукции / Актуальные проблемы современной науки, 2008, № 2, с. 194–195.
2. Локшин А.А . Свободная воля и математика / Знание-Сила, 2010, № 3, с. 86–90. См. также
http://www.inauka.ru/math/article100025.html
3. Ефимов Н.В . Высшая геометрия. – М.: Наука, 1978.
4. Мерзон А.Е., Добротворский А.С., Чекин А.Л. Пособие по математике для студентов факультетов начальных классов. – М., 1998.
5. Козлова Е.Г. Сказки и подсказки. Задачи для математического кружка. – М.: МЦНМО, 2004.
6. Энгелер Э. Метаматематика элементарной математики. – М.: Мир, 1987.
Cм. [1].
Рассуждая аналогично [2], можно показать, что и понятие бесконе ч ность основано на понятии свободы воли.
Не путать с аксиомой выбора!
В свое время аналогичная модель обсуждалась с И. Христовой.
См. предыдущий параграф.

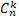 – число сочетаний из n элементов по k элементов, т.е. число различных k - элементных подмножеств n - элементного множества;
– число сочетаний из n элементов по k элементов, т.е. число различных k - элементных подмножеств n - элементного множества;