Надо сказать, что, познакомившись с этим простым рассуждением, студенты были сильно удивлены.
Вообще, на наш взгляд, должен существовать обязательный (и для гуманитариев, и для «технарей») список задач, развивающих воображение. И, пожалуй, задачу о распиливании куба следовало бы в него включить.
Задача . Истинно ли утверждение: <<���Квадрат невозможно разрезать на три квадрата>>?
14. ПОЧЕМУ ДЕЛЕНИЕ
НЕ ДИСТРИБУТИВНО СЛЕВА?
Выпускники школ обычно прекрасно справляются с «раскрытием скобок» в выражениях, где нужно воспользоваться дистрибутивностью умножения относительно сложения и вычитания:
( a ± b )· c = a · c ± b · c , (1)
с ·( a ± b ) = c · a ± c · b (2)
и правильно раскрывают скобки в выражениях вида
( a ± b ): c = a : c ± b : c (3)
(пользуясь дистрибутивностью справа деления относительно сложения и вычитания).
Неприятность, однако, заключается в том, что многие ученики, по аналогии с парой соотношений (1), (2), «раскрывают скобки» и в формулах вида c : ( a ± b ), приравнивая это выражение
c : a ± c : b (что, естественно, является грубой ошибкой). Доказать, что, вообще говоря,
c : ( a ± b ) ≠ c : a ± c : b (4)
очень легко с помощью контрпримера:
20: (4+1) = 4, в то время как 20:4 + 20:1 = 25.
Преподаватель, ограничиваясь подобным контрпримером, предлагает ученикам просто-напросто запомнить , что для умножения имеет место двусторонняя дистрибутивность относительно сложения и вычитания, а для деления – справедлива только дистрибутивность справа. Однако запомненное, но не понятое сведение, как показывает наш педагогический опыт, учениками к концу обучения в школе забывается.
Однако причина отличия пары (1), (2) от (3), (4 ) очень проста и заключается в том, что умножение вещественных чисел коммутативно, а деление – нет. Действительно, из (1) сразу же вытекает соотношение (2) в силу коммутативности умножения ; в то же время из (3) вывести аналогичное равенство невозможно в силу некоммутативности деления. На наш взгляд, сообщать ученикам это простое соображение совершенно необходимо.
15. ОБОБЩЕННАЯ ДИАГРАММА ЭЙЛЕРА
Как хорошо известно, если имеются одно, два или три свойства (которые обозначим ( a ), ( b ), ( c )), характеризующие элементы некоторого множества М, то классы, на которые разбиваются элементы множества М, удобно геометрически представлять на диаграмме Эйлера. Если же число свойств, по которым идет классификация элементов множества М, больше трех, то пользоваться диаграммой Эйлера неудобно. В общем случае, когда рассматриваются n свойств, справедлива следующая теорема (см. [4]): максимальное число различных классов, на которые при п о мощи n свойств может быть разбито множество М, равно 2 n 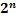 .Этот факт доказывается в [4] из комбинаторных соображений.
.Этот факт доказывается в [4] из комбинаторных соображений.
Заметим, однако, что если с самого начала использовать не диаграмму Эйлера, а предлагаемую ниже ее модификацию, то сформулированная теорема может быть доказана на рисунке. Рассмотрим вначале случай трех свойств; «места» для элементов множества М, обладающих свойством ( a ), будем условно обводить кружком, «места» для элементов, обладающих свойством ( b ) – квадратом; «места» для элементов со свойством ( с ) – треугольником.
Вначале отметим в большом прямоугольнике, изображающем множество М, место для элементов со свойством ( a ) – для этого, очевидно, достаточно нарисовать один кружок . Тем самым элементы из М, в принципе, могут быть разбиты на два класса – на элементы со свойством ( a ) и на элементы без этого свойства (любой из этих классов может быть пуст). Далее, отметим на рисунке места, где в принципе могут располагаться элементы со свойством ( b ): для этого, очевидно, придется нарисовать два квадрата: один внутри кружка и еще один вне кружка. Теперь будем отмечать места для элементов со свойством ( с ): нам, очевидно, придется нарисовать четыре треугольника (см. рис. 15.1). Каждый раз, добавляя возможные места для элементов со следующим новым свойством, мы рисуем в точности столько новых символов, сколько было построено различных возможных классов на предыдущем шаге. Иными словами, на каждом новом шаге число различных возможных классов, отвечающих нашему разбиению, удваивается. Поскольку для одного-единственного свойства ( a ) возможных классов было 2, мы, очевидно, получили наглядное геометрическое доказательство сформулированной выше теоремы.
Читать дальше

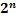 .Этот факт доказывается в [4] из комбинаторных соображений.
.Этот факт доказывается в [4] из комбинаторных соображений.