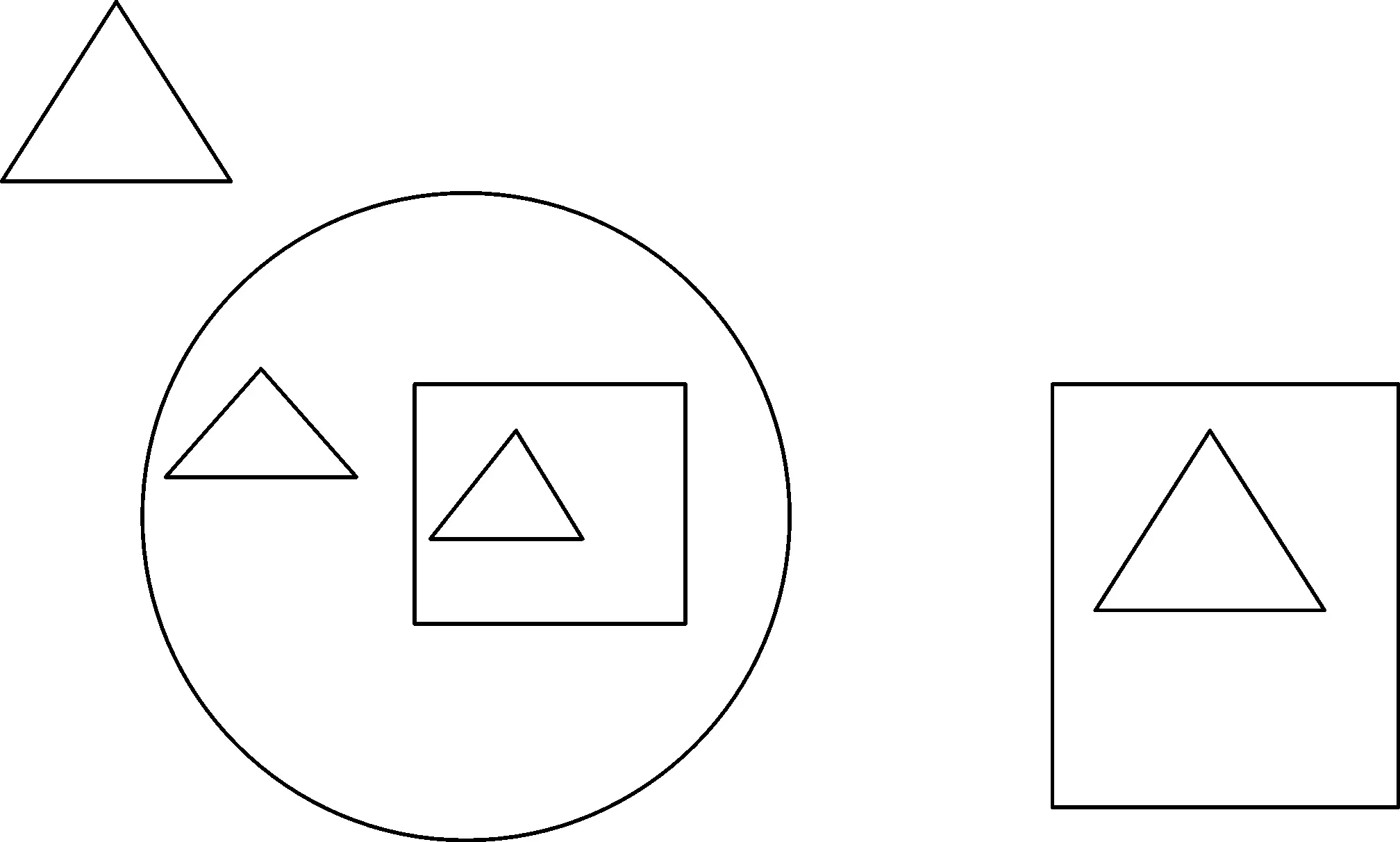
Рис. 15.1
В заключение параграфа приведем задачу, иллюстрирующую связь между классическими диаграммами Эйлера и предложенным их вариантом.
Задача.На острове Буяне расположена пиратская база, где в круглых и прямоугольных башнях содержатся 113 пленников. Круглых башен 7, прямоугольных 10. Три круглые башни – внутри трех прямоугольных, четыре круглые башни – внутри четырех круглых. Семьдесят семь пленников содержатся в круглых башнях, восемьдесят восемь – в прямоугольных. Однажды все 113 пленников сбежали – им удалось перелезть через стены башен. Скольким пленникам пришлось перелезать через две стены?
16. ЗМЕЙ ГОРЫНЫЧ И ТРАНЗИТИВНОСТЬ
Пусть М – некоторое множество (для определенности – конечное). Отношением на множестве М называют закон, который сопоставляет некоторым элементам из М какие-нибудь (другие или те же самые) элементы этого множества.
Таким образом, отношение на множестве – это чрезвычайно общее понятие. Здесь мы напомним лишь некоторые свойства отношений, которые понадобятся для решения приводимой ниже задачи про Змея Горыныча.
Но прежде рассмотрим пример. Пусть М – это множество из 10 человек, а Р – отношение, заданное на М следующим образом:
P: «человек а – брат человека b ».
Тот факт, что «человек а – брат человека b » мы будем коротко записывать в виде: a P b .
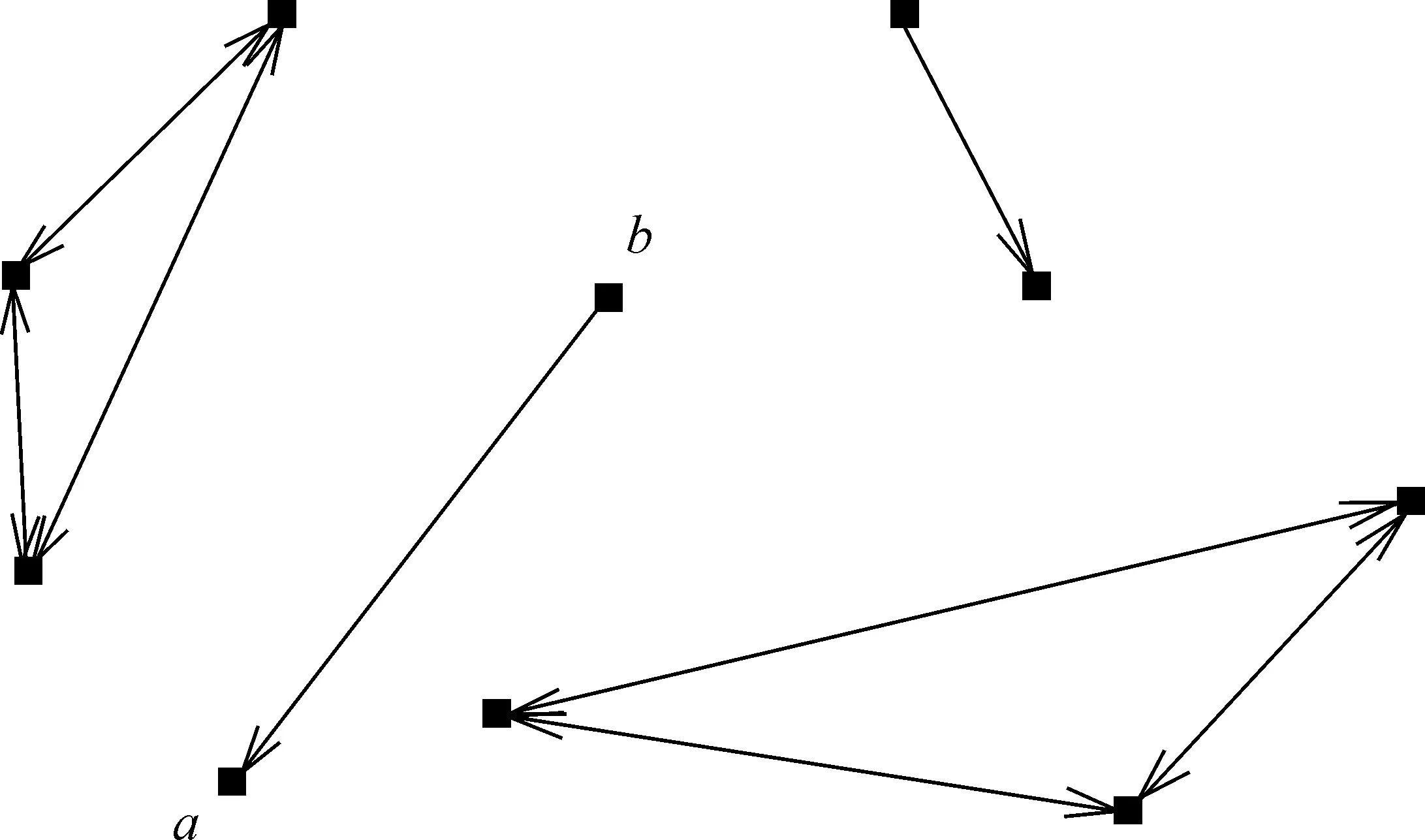
Изобразим теперь элементы нашего множества М в виде точек на плоскости, обозначив их соответственно a,b,c,d,… . При этом, если, например, имеет место соотношение a P b , из точки a проведем стрелку к точке b и с другими точками поступим аналогичным образом (см. рис. 16.1). Рисунок, который у нас получился, называется графом отношения P.
Упражнение.Как объяснить, что на рис. 16.1 некоторые стрелки заострены с двух сторон, а некоторые – только с одной?
Определение 1.С кажем, что отношение Р (заданное на некотором множестве М) асимметрично , если ни для какой пары элементов a,b из множества М не может одновременно быть a P b
и b P a .
На графе асимметричного отношения, очевидно, никакие стрелки не могут быть заострены с двух сторон.
Рис. 16.1
Определение 2.Скажем, что отношение Р, заданное на множестве М, транзитивно , если для любых трех элементов a,b,c
из М одновременная справедливость a P b и b P c влечет за собой справедливость а P c .
На графе транзитивного отношения, таким образом, одновременно с составным путем (вдоль стрелок), идущим из a в c через b, cуществует стрелка, непосредственно идущая из a в c .
Определение 3.Отношение Р, заданное на множестве М, называется связным , если для любых двух элементов a , b из М справедливо хотя бы одно из двух соотношений: a P b , b P a.
Определение 4.Отношение Р задает на множестве М лине й ный порядок , если оно асимметрично, транзитивно и связно.
Пример.Пусть множество М состоит из n человек. Очевидно, что линейно упорядочить множество М – это поставить людей, составляющих данное множество, в очередь друг за другом. Заметим, что в силу правила произведения из n людей можно образовать n ! различных очередей.
Преподавая тему «Отношения на множестве», авторы столкнулись с некоторым дефицитом интересных, но несложных задач. Предлагаемая ниже задача представляет собой попытку компенсировать упомянутый дефицит.
Задача 1.В стране Карабасии N городов, причем каждый город соединен с каждым дорогой с односторонним движением (направление движения показано стрелкой на специальных дорожных указателях). Однажды ночью в Карабасию прилетел Змей Горыныч и переставил указатели так, что на следующее утро ни один из жителей Карабасии, выехавший из своего города, не смог потом вернуться домой. Требуется выяснить:
Читать дальше