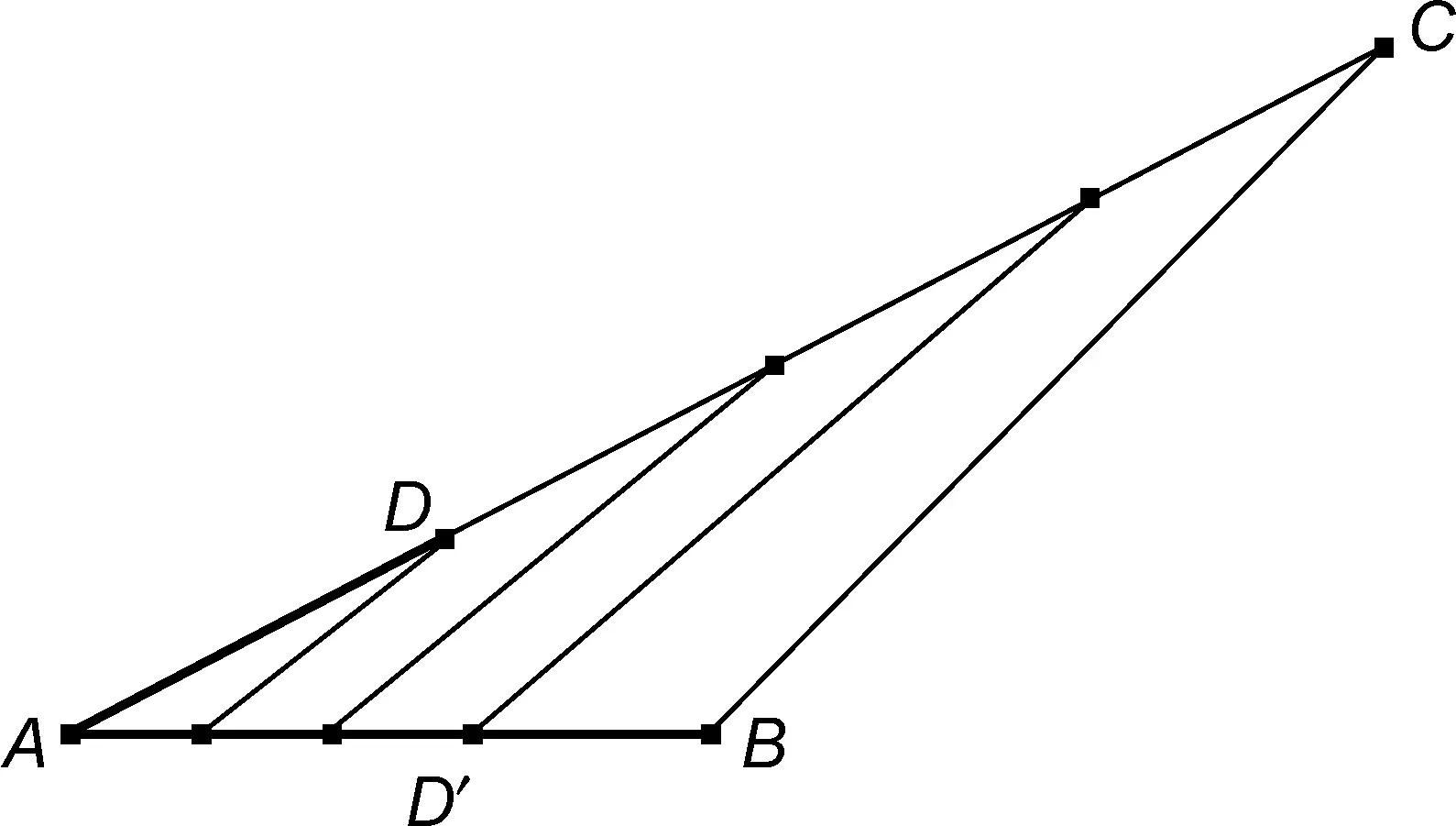
2. Пересадим «лишнего» соловья на первую елку, на ней теперь два соловья.
3. Пересадим теперь соловья с последней елки на вторую елку. На второй елке теперь тоже два соловья. А на последней елке – ни одного!
4. Никакие елки, кроме первой, второй и последней уже не нужны. Трех елок хватило, чтобы выполнить все условия задачи.
Ответ:три елки, четыре соловья.
В заключение приведем еще одну задачу, также не допускающую моделирование «в отрезках», но легко решаемую при помощи мысленного моделирования.
Задача 3.В школьном саду посадили клены по 16 штук в каждом ряду и столько же лип по 20 штук в каждом ряду, причем рядов получилось на 2 меньше. Во сколько рядов посажены клены?
Решение алгебраическое.Пусть х – количество рядов из кленов, у – количество рядов из лип. Тогда имеем систему:
у = х – 2, (5)
16 х = 20 у . (6)
Подставляя выражение для у из (5) в (6), получаем
16 х = 20( х – 2), откуда х = 10.
Нетрудно видеть, однако, что (непосредственно, без предварительных алгебраических преобразований) при помощи моделирования «в отрезках» система (5), (6) не решается.
Решение арифметическое (основанное на мысленном м о делировании).Будем пересаживать липы так, чтобы они были посажены такими же рядами, как клены. Для этого выкопаем 4 липы из первого ряда и посадим их в новый ряд за последним рядом лип. Чтобы заполнить первый новый ряд, нужно выкопать по 4 липы из первых четырех старых рядов. Чтобы заполнить второй новый ряд нужно выкопать по 4 липы из следующих четырех старых рядов. Поэтому, посадив липы так же как клены, мы образуем 4 + 4 + 2 рядов.
Ответ:клены были посажены в 10 рядов.
Итак, мы видим, что достаточно обширный класс задач, не поддающийся решению при помощи моделирования «в отрезках», может быть решен арифметическим способом при помощи мысленного моделирования. Этот класс задач, безусловно, должен предшествовать в курсе математики задачам, которые рассчитаны на решение алгебраическим способом.
Замечание.В заключение попробуем охарактеризовать задачи, которые могут быть решены при помощи моделирования «в отрезках».
Прежде всего, это задачи, которые сводятся к системе из двух уравнений с диагональной матрицей (коэффициенты системы предполагаются целочисленными). Иными словами – это системы относительно неизвестных х , у вида
x = p , (7)
mx + ny = q . (8)
Системы вида
x = ay , (9)
bx + cy = d , (10)
(где a , b , c , d – целочисленные коэффициенты) также непосредственно, т.е. без предварительного применения алгебраических преобразований, поддаются решению при помощи моделирования «в отрезках». Обе системы (7), (8) и (9), (10) характеризуются тем, что отрезок, изображающий одно из неизвестных (х или у) может быть выбран с самого начала произвольным обр а зом .
5. УСОХШИЕ ПРОЦЕНТЫ
В этом параграфе мы разберем еще одну известную текстовую задачу – «на проценты». Алгебраическое решение этой задачи, как правило, вызывает у учеников недоумение и воспринимается ими в известной мере формально.
Задача.В магазин привезли 100 килограммов ягод, влажность которых составляла 99%. Через некоторое время ягоды немного подсохли, и их влажность стала равна 97%. Сколько стали весить ягоды, привезенные в магазин?
Решение.Обозначим через х вес сухого вещества ягод. Имеем из условия:
х = 100 – 100·0,99 = 1 (кг). (1)
После усушки вес сухого вещества ягод, очевидно, не изменился, поэтому, обозначая через у (общий) вес ягод после усушки, очевидно, приходим ко второму уравнению:
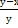 (2)
(2)
Разрешая систему (1), (2) относительно у, неожиданно получаем:
Ответ:После усушки ягоды стали весить кг.
Итак, усохнув всего-навсего на 2%, ягоды стали почему-то весить втрое меньше…
Продвинутые ученики, понимают, конечно, в чем тут дело, но остальным полученный ответ кажется очень странным и даже неверным.
Тем самым возникает чисто педагогическая проблема – как изложить решение этой задачи, чтобы ее ответ сделался не странным, а, напротив, очевидным?
Рис. 5.1
Как показывает опыт, делу может помочь следующая геометрическая модель (которую, впрочем, редко используют [4] В свое время аналогичная модель обсуждалась с И. Христовой.
); см. рис. 5.1, где условно принято:
Читать дальше

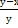 (2)
(2)