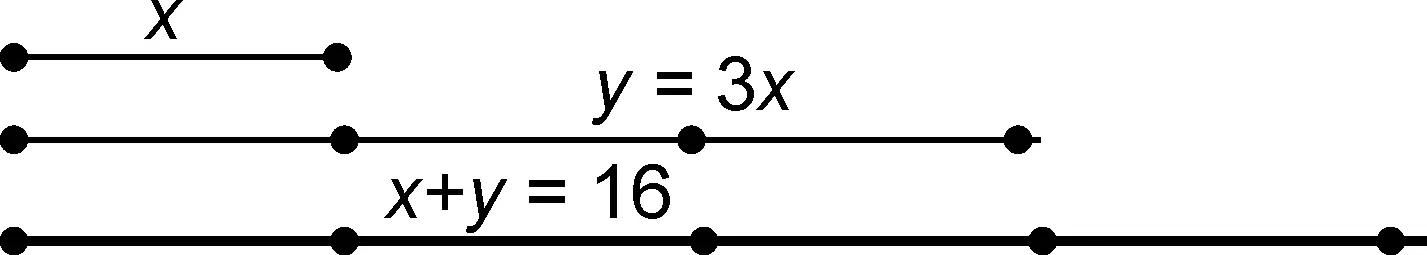A.A. Lokshin - Аннотация

Задача Б.Десять мышек и птичек (птички и мышки настоящие, не игрушечные) съели 56 зерен. Каждая мышка съела 5 зерен, а каждая птичка – 6 зерен. Сколько было мышек и сколько птичек?

Решение (алгебраическое).Пусть x – число мышек, y – число птичек. Составляем соответствующую задаче Б систему уравнений, содержащих именованные величины:

x + y = 10 (животных), 5 x + 6 y = 56 (зерен). Опуская имена величин, приходим к системе

x + y = 10, 5 x + 6 y = 56. (**)

Решая ее, получаем: x = 4, y = 6.

Ответ:4 мышки, 6 птичек.

Система (**) формально совпадает с системой (*) и решается тем же способом, что и система (*). Однако, как показывает наш опыт, дети, решив сначала задачу А алгебраическим способом и дав своему решению правильное истолкование на языке наглядных образов, затруднялись объяснить смысл аналогичных преобразований системы (**). Некоторые говорили так: «Нужно взять пять комплектов животных и вычесть их из 56 зерен…» Причина затрудн е ний, очевидно, была в том, что уравнения системы (**) , в отличие от системы (*) , содержат величины разных наимен о ваний .

На наш взгляд, на начальном этапе обучения область применения алгебраического метода должна быть ограничена текстовыми задачами, решение которых не приводит с системам, содержащим величины разных наименований.

Моделирование «в отрезках», используемое в системе Л.Г. Пе-

терсон, существенно облегчает детям понимание текстовых

задач, в значительной степени устраняет случайное манипулирование числовыми данными.

В то же время, у некоторых детей складывается представление о том, что моделирование в отрезках есть универсальный метод, пригодный для решения «всех задач».

Мы ограничимся здесь рассмотрением текстовых задач для начальной школы, не включающим в себя задачи «на движение».

Эти задачи, как правило, сводятся к системе двух уравнений с двумя неизвестными.

Задача 1.В первый день портной сшил несколько костюмов, а во второй день сшил их в три раза больше. Сколько костюмов сшил портной в первый день, если за два дня он сшил их 16?

Решение.Пусть х – количество костюмов, сшитых в первый день, у – количество костюмов, сшитых во второй день. В результате имеем систему из двух уравнений специального вида:

у = 3 х , (1)

х + у = 16. (2)

Совершенно очевидно, что алгебраическая процедура решения этой системы в точности соответствует процедуре решения при моделировании «в отрезках» (см. рис. 4.1).

Однако, научить ребенка мыслить – это, в сущности, на у чить его строить разнообразные модели. Наш педагогический опыт показывает, что желательно познакомить детей с задачами, для которых модели «в отрезках» не работают и которые, тем не менее, могут быть решены с помощью несложных и наглядных рассуждений. (Что касается алгебраического подхода к решению текстовых задач, то он, позволяя быстро получить ответ при помощи стандартных операций с символами, не способствует развитию образного и логического мышления.)

Задача 2(см., например, [5]). Когда на каждую елку село по одному соловью, то один соловей остался без елки. А когда соловьи расселись на елках парами, то одна елка осталась без соловьев. Сколько было елок и сколько было соловьев?

Решение алгебраическое. Пусть х – количество соловьев, у – количество елок. В результате имеем систему из двух уравнений:

х = у + 1, (3)

х = ( у – 1)·2. (4)

Подставляя х из (3) в (4), получаем

у + 1 = 2 у – 2, (4)

откуда у = 3, х = 4.

Попробуем теперь решить эту же задачу при помощи «моделирования в отрезках». Соотношение (3), конечно, может быть изображено графически; однако, после того как масштаб на рисунке, изображающем соотношение (3), выбран, соотношение (4) изобразить «в отрезках» уже не удается. (Точно так же без пре д варительных алгебраических преобразований не удается изобразить «в отрезках» и равенство (4).)

Решение арифметическое (основанное на мысленном м о делировании).

1. Представим себе ряд из нескольких елок. На каждой сидит по соловью. Один соловей – «лишний», он висит в воздухе рядом с последней елкой – для него не хватило елки.