AC = 100 (кг), AB = y (кг),
AD = AD = 1 (кг),
AD = 1% AC , AD = 3% AB .
Глядя на этот рисунок, даже слабые ученики воспринимают тот факт, что если отрезок AD составляет сотую долю извес т ного отрезка AC, а отрезок, составляющий сотую долю от AB, в три раза короче, чем AD, то:
AB =  AC, и тем самым AB =
AC, и тем самым AB = 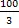 = (кг).
= (кг).
В результате обращения к этой геометрической модели, задача оказывается не формально «пройденной», а действительно понятой учениками.
6. ПРАВИЛО ПРОИЗВЕДЕНИЯ
В КОМБИНАТОРНОЙ ЗАДАЧЕ О МАРШРУТАХ
Хорошо известно следующее правило комбинаторики – так называемое правило произведения. Если нужно выбрать упорядоченную пару элементов ( a , b ) и первый элемент пары можно выбрать
k способами, а после того как первый элемент выбран, второй элемент можно выбрать m способами, то упорядоченную пару, состоящую из этих двух элементов, можно выбрать k ∙ m способами.
Доказывается это очень просто. Будем изображать возможный выбор первого элемента пары ( a , b ) в виде ствола дерева
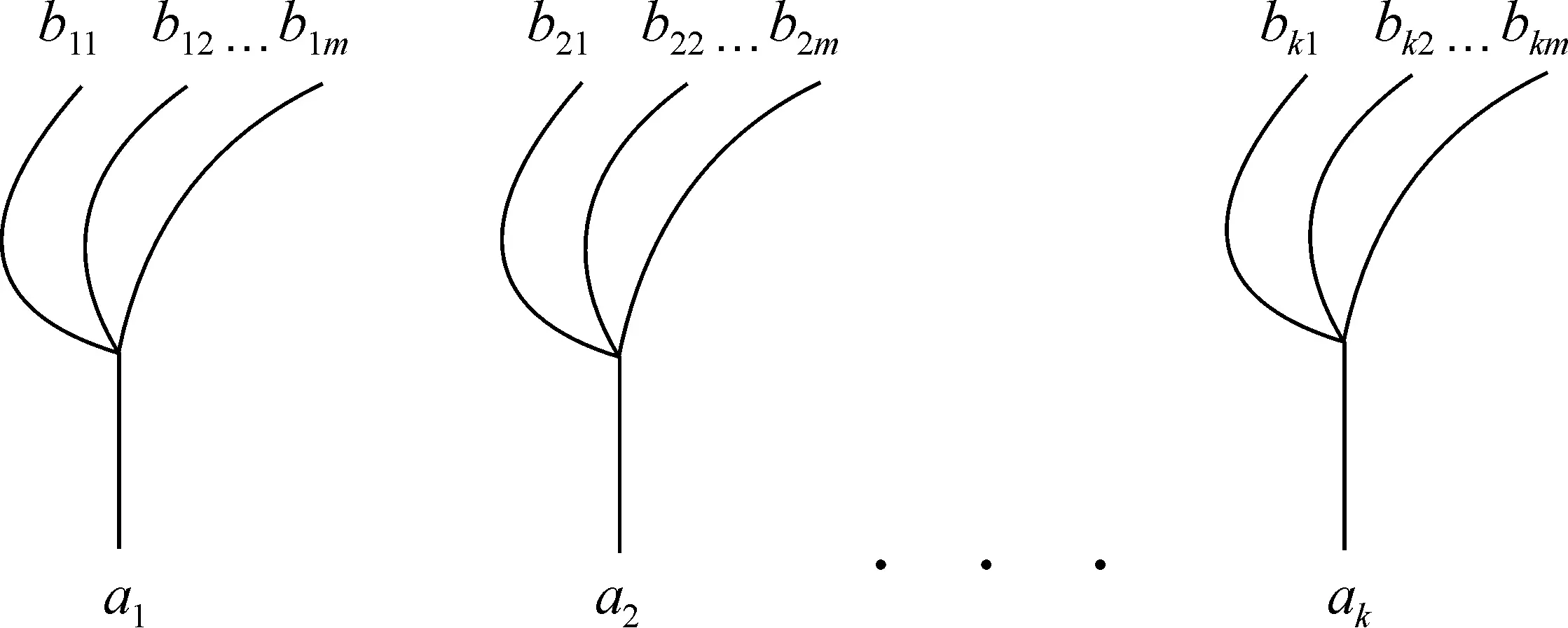
(см. рис. 6.1), а возможный выбор второго элемента пары – в виде ветки, растущей из верхнего конца ствола (см. рис. 6.2).
Рис. 6.1
Рис. 6.2
Тогда выбору упорядоченной пары вида ( a , b ) будет соответствовать маршрут от «подножия» одного из k деревьев до верхушки ствола и затем по одной из m веток до самого верха. Нетрудно видеть, что всего таких маршрутов будет
m + m + … + m = m∙k (1)
(слева в (1) k слагаемых). Маршруты мы считаем различными, если они не совпадают хотя бы в одной из своих частей.
Возможна ситуация, когда, например, 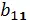 b 11 = b 21
b 11 = b 21 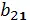 , но в этом случае нам приходится сравнивать маршруты ( a 1, b 11) и ( a 2, b 21), а они различны, ибо
, но в этом случае нам приходится сравнивать маршруты ( a 1, b 11) и ( a 2, b 21), а они различны, ибо 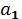 a 1 ≠
a 1 ≠ 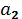 a 2 по предположению.
a 2 по предположению.
Правило произведения легко обобщается на случай, когда требуется сосчитать число возможных способов выбрать упор я доченную тройку элементов или, более общо, упорядоченный н а бор из n элементов.
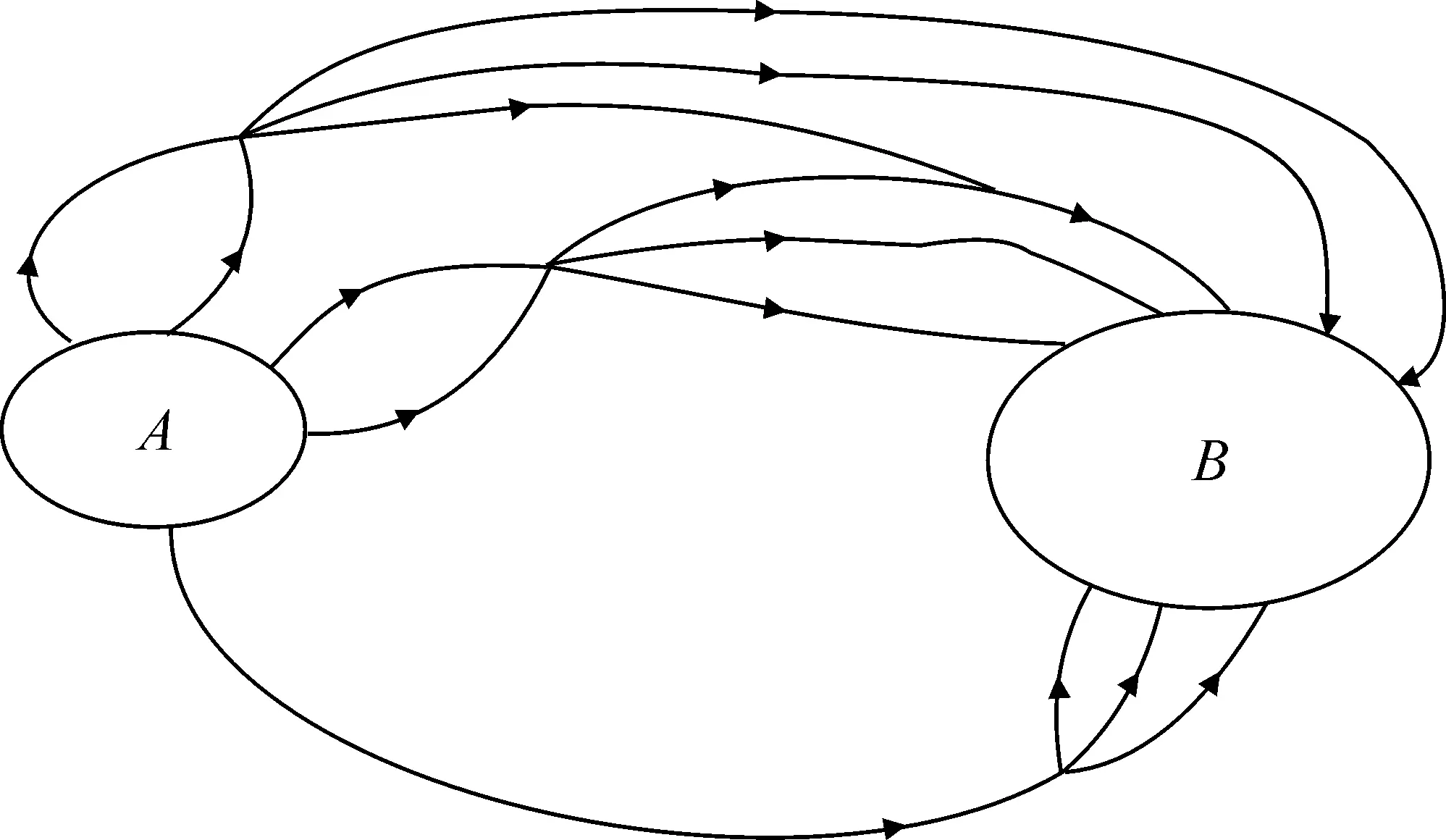
Применим теперь правило произведения к решению простейшей задачи. Пусть города А и В связаны сетью дорог, как показано на рис. 6.3.
Ехать из А в В можно только по направлениям, указанным стрелками (так что мы, по существу, имеем дело с ориентированным графом). Спрашивается, сколькими способами можно доехать из А в В ? Нетрудно видеть, что выбор первого участка маршрута (до развилки) можно осуществить пятью способами, после чего выбрать второй участок пути всегда (т.е. при любом выборе первого участка) можно тремя способами. Таким образом, применимо правило произведения, и общее количество способов, которыми можно добраться из А в В , равно 5∙3 = 15.
Поставим теперь следующий вопрос: а сколькими способами можно вернуться из В в А ? (Разрешается ехать только против направления стрелок на рис. 6.3).
Рис. 6.3
Из рис. 6.3 очевидно, что правило произведения «в обратную сторону» не работает. Тем не менее, понятно, что каждому маршруту из А в В соответствует в точности один маршрут из В в А (мы увидим этот маршрут, если «прокрутим киноленту» в обратном направлении). Значит, вернуться из В в А можно по-преж-
нему 15-ю способами.
Любопытно, что в задачах о маршрутах возникает ситуация, в которой подсчет числа вариантов по-прежнему можно проводить по правилу произведения, но выбор «упорядоченной пары элементов» уже не столь очевиден, как раньше.
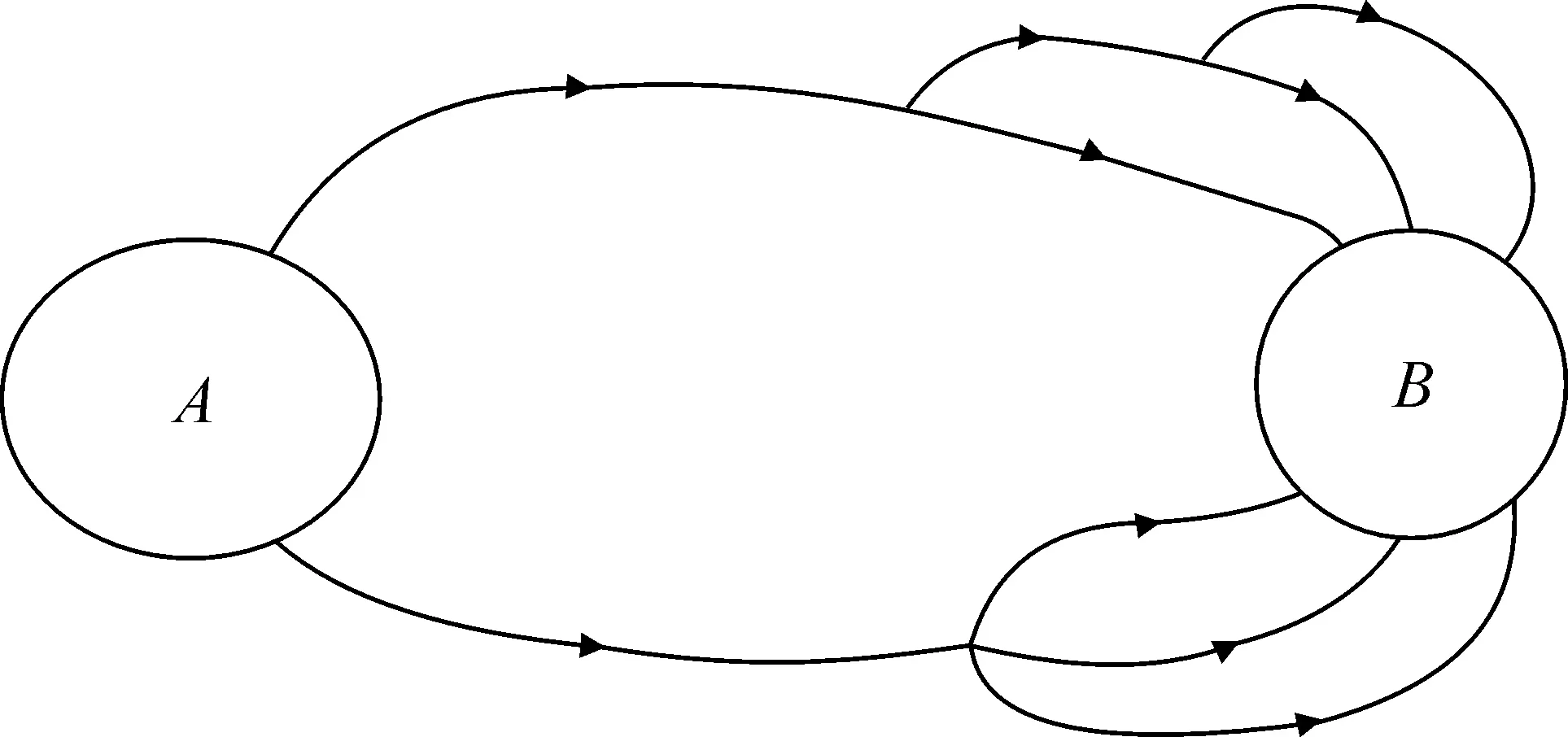
А именно, пусть на этот раз города А и В связаны сетью дорог, изображенной на рис. 6.4.
Рис. 6.4
Понятно, что в качестве упорядоченной пары ( a, b ) здесь следует брать пару: (малый начальный участок маршрута, малый конечный уч а сток маршрута).
Читать дальше

 AC, и тем самым AB =
AC, и тем самым AB = 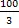 = (кг).
= (кг).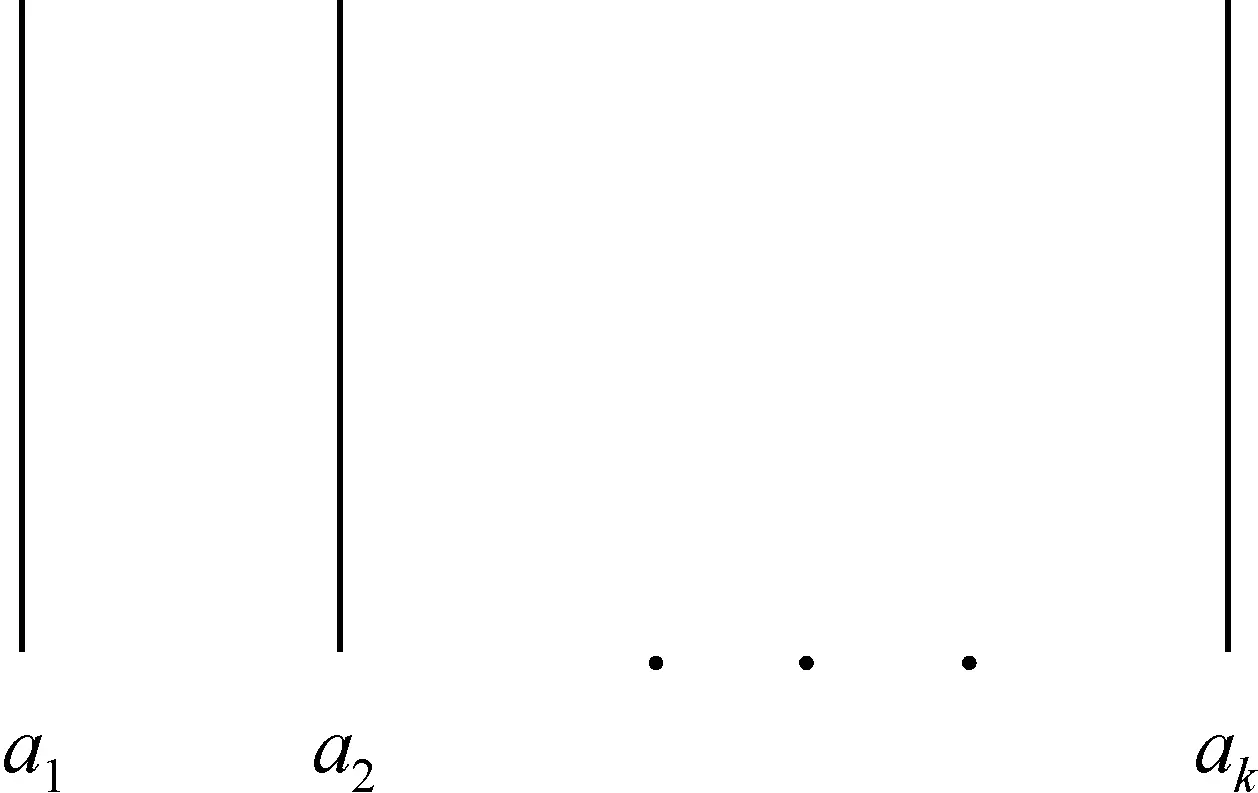
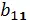 b 11 = b 21
b 11 = b 21 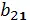 , но в этом случае нам приходится сравнивать маршруты ( a 1, b 11) и ( a 2, b 21), а они различны, ибо
, но в этом случае нам приходится сравнивать маршруты ( a 1, b 11) и ( a 2, b 21), а они различны, ибо 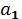 a 1 ≠
a 1 ≠ 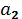 a 2 по предположению.
a 2 по предположению.