О. ОРЕ - Приглашение в теорию чисел

m 1= m 2, n 1=, D ( m, n ) = 1. (5.2.6)

Здесь мы можем без нарушения общности считать, что m > 0, n > 0. Теперь подставим m 2и n 2вместо m 1и n 1 соответственно в уравнения (5.2.3) и (5.2.4);

получим

m 2= 1/2 z + 1/2 y, n 2= 1/2 z — 1/2 y, m 2 n 2= 1/4 x 2,

т. е.

x = 2 mn, y = m 2— n 2, z = m 2+ n 2. (5.2.7)

Проверка показывает, что эти три числа всегда удовлетворяют соотношению Пифагора х 2 + у 2= z 2.

Осталось определить, какие целые положительные числа m и n в действительности соответствуют простейшим треугольникам. Докажем, что следующие три условия на числа m и n являются необходимыми и достаточными:

(1) ( m, n ) = 1,

(2) m > n , (5.2.8)

(3) одно из чисел m и n четное, а другое — нечетное.

Доказательство . Сначала покажем, что если числа х, у, z образуют простейшую тройку, то условия (5.2.8) выполняются. Мы уже показали, что условие (1) является следствием того, что числа х, у, z взаимно простые. Условие (2) следует из того, что числа х, у, z — положительны. Чтобы увидеть, что условие (3) необходимо, заметим, что если m и n оба нечетные, то в соответствии с (5.2.7) у и z были бы оба четные, в противоречие с результатами, полученными в конце предыдущего параграфа.

Наоборот, если условия (5.2.8) выполнены, то соотношения (5.2.7) определяют простейшую тройку: условие (2) обеспечивает положительность чисел х, у и z .

Могут ли какие-нибудь два из этих трех чисел иметь общий простой множитель р ? Такое простое число р , делящее два из них, должно также делить и третье в силу соотношения х 2+ у 2= z 2. Если число р делит х , то оно в соответствии с (5.2.7) должно делить 2 mn . Число р не может равняться 2, потому что у и z нечетные в соответствии с условием (3) и (5.2.7). Предположим, что р ≠ 2 — нечетное простое число, делящее m . Тогда условие (1) и выражение (5.2.7) показывают, что р не может делить у и z . Такие же рассуждения применимы и для случая, если р делит число n .

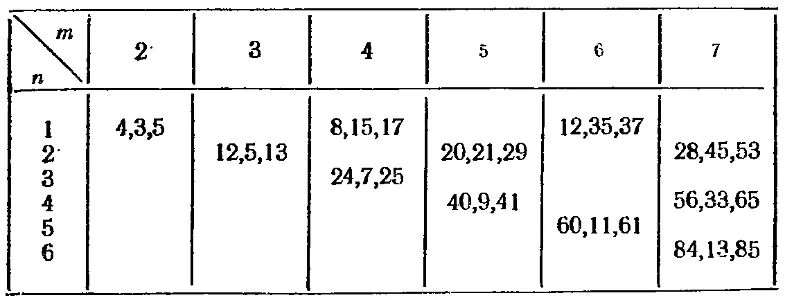
Найдя необходимые и достаточные условия (5.2.8) для того, чтобы m и n давали простейший треугольник, можно вычислить все такие треугольники с помощью соотношения (5.2.7). Например, пусть

m = 11, n = 8.

Наши условия выполнены, и мы находим, что

х = 176, у = 57, z = 185.

В табл. 3 приведены все простейшие треугольники х, у, z для нескольких первых значений чисел т и n .

Таблица 3

Система задач 5.2.

1. Продлите таблицу для всех значений m ≤ 10.

2. Могут ли два разных набора значений чисел m и п , удовлетворяющих условию (5.2.8), дать один и тот же треугольник?

3. Найдите все пифагоровы треугольники, у которых длина гипотенузы не превосходит 100.

Мы решили задачу нахождения всех треугольников Пифагора. Здесь, как почти всегда в математике, решение одной задачи приводит к постановке ряда других задач. Часто новые вопросы оказываются значительно более трудными, чем первоначальный.

Одним из естественных вопросов о простейших треугольниках является следующий. Пусть задана одна из сторон простейшего треугольника Пифагора, как найти остальные? Первым рассмотрим случай, когда известна сторона у . В соответствии с (5.2.7)

y = m 2— n 2= ( m + n )( m — п ), (5.3.1)

где m и n —числа, удовлетворяющие условиям (5.2.8).

В уравнении (5.3.1) множители ( m + n ) и ( m — n ) взаимно простые. Чтобы в этом убедиться, заметим, что эти множители

а = m + n, b = m — n (5.3.2)

оба нечетные, так как одно из чисел m и n нечетное, а другое четное. Если числа а и b имеют общий нечетный простой множитель р , то число р должно было бы делить каждое из чисел

а + b = m + n + ( m — n ) = 2 m

и

а — b = m + n — ( m — n ) = 2 n ,

т. е. р должно было бы делить числа m и n . Но это невозможно, так как D ( m, n ) = 1.

Предположим теперь, что есть разложение данного нечетного числа у на два множителя

y = a b, a > b, D ( a, b ) = 1. (5.3.3)

Из (5.3.2) получаем

m = 1/2 ( a + b ), n = 1/2 ( a — b ). (5.3.4)