О. ОРЕ - Приглашение в теорию чисел

Доказательство. Так как число с делит произведение ab , то простые множители числа с содержатся среди простых множителей чисел а и b . Но так как D ( b, c ) = 1, то их не может быть среди множителей числа b . Таким образом, все простые множители числа с делят число а , но не делят число b , и они появляются в числе а в степенях, не меньших, чем в числе с , так как число с делит ab .

Позже мы используем другой факт.

Если произведение двух взаимно простых чисел является квадратом,

ab = c 2 , D ( a, b ) = 1, (4.2.5)

то числа а и b являются квадратами:

а = а 1 2 , b = b 1 2. (4.2.6)

Доказательство. Для того чтобы некоторое число было квадратом, необходимо и достаточно, чтобы все степени в разложении его на простые множители были четными. Так как числа а и b — взаимно простые (4.2.5), то любой простой множитель из с 2содержится либо в а , либо в b , но не в обоих; отсюда простые множители чисел а и b должны иметь четные степени.

Система задач 4.2.

1. Какие числа взаимно простые с числом 2?

2. Почему D ( n, n + 1) = 1?

3. Исследуйте пары дружественных чисел в табл. 2 (стр. 45) и найдите те из них, которые взаимно просты.

4. Может ли правило, выраженное в формулах (4.2.5) и (4.2.6), быть справедливым не только для квадратов, но и для произвольных степеней?

Вновь вернемся к нашим дробям а / b . Если а > b , то дробь является числом, большим 1, и мы часто разделяем ее на целую часть и правильную дробь, меньшую единицы.

Примеры . Мы пишем

32/5 = 6 + 2/5 = 6 2/5, 63/7 = 9 + 0/7 = 9.

В общем случае мы используем деление с остатком

чисел а и b ( a ≥ b ), а именно:

a = qb + r , где 0 ≤ r ≤ b —1. (4.3.1)

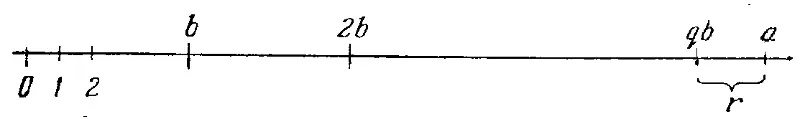
Рис. 14.

Очевидно, что это всегда возможно. Действительно, рассмотрим числа 0, 1, 2… на числовой прямой (рис. 14). Где-то на этой прямой расположено число а . Начиная от точки 0 станем отмечать точки b , 2 b , З b и т. д. до точки qb такой, что qb не больше, чем а , в то время как ( q + 1) b уже больше а . Расстояние от точки qb до точки а и есть r . Мы называем число r остатком при делении (4.3.1), a q — частным . Это частное q встречается столь часто, что имеется специальный символ для его обозначения:

q = [ a/b ].

Этот символ обозначает наибольшее целое число, не превосходящее числа а/b . Для примеров, приведенных выше, получим

[32/5] = 6, [63/7] = 9.

В предыдущем разделе мы исследовали наибольший общий делитель двух натуральных чисел а и b :

d 0= D ( a, b ). (4.3.2)

Чтобы найти число d 0, мы полагали, что мы знаем разложения чисел а и b на простые множители. Однако нахождение таких разложений может оказаться очень трудным занятием для больших чисел. Существует совсем другой метод для нахождения наибольшего общего делителя, который не использует подобных разложений. Он основан на следующем:

Если a = qb + r, где 0 ≤ r ≤ b—1, то

D(a, b) = d = D(r, b). (4.3.3)

Доказательство. Запишем

d 0= D ( a, b ), d 1= D(r, b).

Таким образом, доказательство соотношения (4.3.3) означает доказательство того, что d 0= d 1. Любой общий делитель чисел а и b также делит число

r = а — qb .

Следовательно, число r делится на d 0.

Так как число d 0является делителем как числа r , так и числа b , то оно должно делить и число d 1= D ( b, r ); отсюда d 1≥ d 0. С другой стороны, в соответствии с соотношением (4.3.1) любой общий делитель чисел r и b делит число а , откуда число d 1делит число а . Так как число d 1делит также и число b , то оно должно делить и число d 0= D ( a, b ), следовательно, d 0≥ d 1. Из сказанного следует, что d 0= d 1.

Пример. 1066 = 5 • 200 + 66; следовательно, (1066, 200) = (66, 200).

Этот результат, сформулированный в утверждении (4.3.3), дает нам простой метод вычисления наибольшего общего делителя двух чисел. Вместо поисков наибольшего общего делителя чисел а и b достаточно найти наибольший общий делитель чисел r и b . Эта задача более проста, так как число r меньше, чем каждое из чисел а и b . Чтобы найти наибольший общий делитель чисел r и b , мы вновь воспользуемся тем же методом и разделим число b на r :