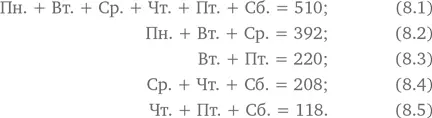Альфред Позаментье - Стратегии решения математических задач. Различные подходы к типовым задачам

Более рациональный подход к этой задаче предполагает анализ с использованием визуального представления. Нарисуем календарь и просто поставим инициалы молодых людей в клетках с теми датами, в которые они работают.

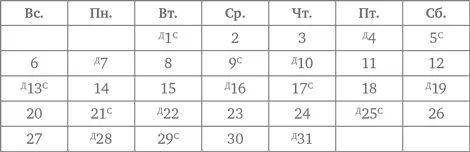
В те даты, где стоят инициалы обоих молодых людей, они работают вместе. На рисунке эти даты ясно видны: 13 и 25 марта.

Эту задачу можно решить еще одним способом, если посмотреть на нее с другой точки зрения. Известно, что числа 4 и 3 являются взаимно простыми и представляют количество дней в рабочем цикле каждого молодого человека, соответственно. Их общее кратное, 12, дает дни между датами, в которые они работают вместе. Таким образом, 1 + 12 = 13 — это день, когда молодые люди работают вместе после первого дня, а 13 + 12 = 25 — это день, в который они работают вместе в следующий раз.

На местной ярмарке несколько работников занимаются отслеживанием количества людей, принимающих участие в конкретных мероприятиях каждый день. Записи Розалинды показывают, что с понедельника до субботы включительно стенд для стрельбы из лука посетили 510 человек. По подсчетам Габиэля с понедельника по среду включительно на этом стенде побывали 392 человека, а Фрэнк насчитал там во вторник и в пятницу 220 человек. Адель работала в среду, четверг и субботу и у нее получилось в сумме 208 человек. Наконец, в записях Альфреда значилось, что с четверга по субботу включительно на стенде побывали 118 человек. Если предположить, что все эти данные правильны, то сколько человек посетили стенд для стрельбы из лука в понедельник?

Как правило, начинают составлять ряды уравнений, в которых переменные представляют разные дни недели. В результате получается пять уравнений первой степени с шестью неизвестными. Конечно, не все неизвестные встречаются в каждом уравнении.

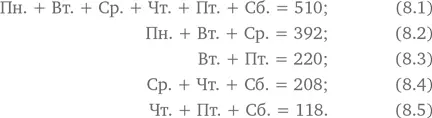
Решив эту систему уравнений, можно попытаться найти ответ. Однако этот процесс довольно сложен и большинству не под силу. (Мало кто догадывается, что в результате вычитания уравнений 8.3 и 8.4 из уравнения 8.1 получается Пн. = 82.)

Визуализируем условия задачи в виде таблицы посещаемости стенда:

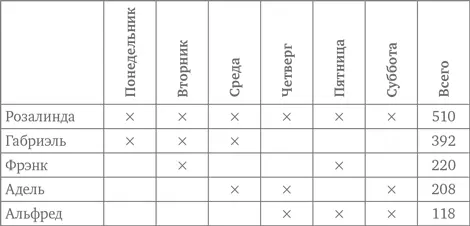
Обратите внимание на то, что за исключением понедельника каждый день упоминается три раза. Это приводит к двойному учету посетителей четырьмя последними учетчиками во все дни кроме понедельника. Таким образом, мы получаем одно уравнение:

2 × 510 − (392 + 220 + 208 + 118) = количество посетителей в понедельник; 1020 − 938 = 82.

В понедельник стенд посетили 82 человека.

Аманда, Айан, Сара и Эмили выставили своих лягушек для участия в соревнованиях на дальность прыжка на ярмарке. Лягушка Аманды опередила лягушку Эмили, но оказалась не первой. Лягушка Сары проиграла лягушке Аманды, но была не последней. Как распределились места лягушек?

Чаще всего берут четыре фишки, жетона или монеты, наклеивают на них стикер с именем владельца и переставляют этих «лягушек» до тех пор, пока результат не будет удовлетворять условиям задачи.

Эту задачу проще решить с использованием визуального представления. Прежде всего, мы знаем, что лягушка Аманды опередила лягушку Эмили, но была не первой. Обозначим это схематично так:

Лягушка Сары проиграла лягушке Аманды, но была не последней. Продолжив построение схемы, мы получаем следующее распределение мест:

Схема позволила легко увидеть порядок, в котором распределились места.

Из 40 мальчиков в оздоровительном лагере «Кэмп-Уолден» 14 участвовали в заплыве на озере, 13 играли в баскетбол, а 16 ходили в поход. Трое мальчиков играли в баскетбол и участвовали в заплыве. Пять мальчиков участвовали в заплыве и ходили в поход. Восьмеро мальчиков играли в баскетбол и ходили в поход, а двое мальчиков участвовали во всех трех спортивных мероприятиях. Сколько мальчиков в этом лагере не участвовали ни в чем?