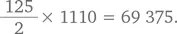Джером открыл свое первое предприятие по прокату каяков. За прокат он берет почасовую оплату. Каякам присваиваются идентификационные номера, на каждом из них стоят три цифры. Первая цифра — это номер предприятия, а именно 1. Номера у каяков не могут повторяться, а три цифры должны располагаться в возрастающем порядке. Ноль использовать нельзя. Вскоре Джером обнаружил, что использовал все возможные сочетания, которые удовлетворяют условиям. Какое максимальное количество каяков может быть у Джерома?
Самый распространенный подход — выписывание всех возможных трехзначных чисел, удовлетворяющих условиям задачи. Но как узнать, все ли эти числа учтены? Существует ли метод, обеспечивающий гарантированное решение? Обычный подход явно не самый эффективный!
Представим наши данные в табличной форме:
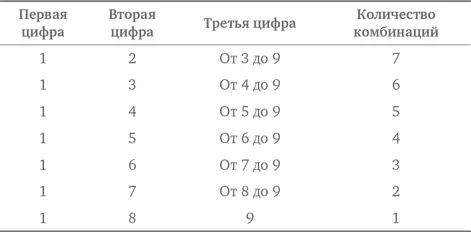
Джером может иметь не более чем 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28 каяков.
Фермер везет яблоки на рынок. Яблоки уложены в шесть ящиков. Весы на пункте взвешивания могут принять за раз только пять ящиков. Нам дают результаты шести взвешиваний:
Ящик B + ящик C + ящик D + ящик E + ящик F = 200 фунтов;
Ящик A + ящик C + ящик D + ящик E + ящик F = 220 фунтов;
Ящик A + ящик B + ящик D + ящик E + ящик F = 240 фунтов;
Ящик A + ящик B + ящик C + ящик E + ящик F = 260 фунтов;
Ящик A + ящик B + ящик C + ящик D + ящик F = 280 фунтов;
Ящик A + ящик B + ящик C + ящик D + ящик E = 300 фунтов.
Сколько фунтов яблок в каждом ящике?
Эту задачу можно решить алгебраически, составив шесть уравнений с шестью неизвестными:
B + C + D + E + F = 200;
A + C + D + E + F = 220;
A + B + D + E + F = 240;
A + B + C + E + F = 260;
A + B + C + D + F = 280;
A + B + C + D + E = 300.
Решение шести уравнений довольно трудоемко, поэтому попробуем поискать другой подход к этой задаче.
С помощью нашей стратегии организации данных можно упростить решение задачи и сделать его изящным. Начнем с представления данных в табличной форме:
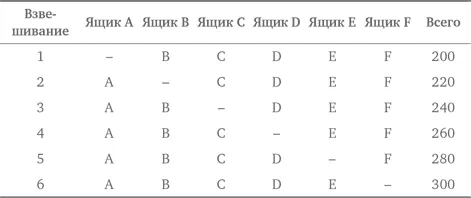
Мы опять получили довольно громоздкий набор уравнений, но можно посмотреть на них с другой точки зрения и организовать данные вертикально, просуммировав колонки в вертикальном направлении:
5A + 5B + 5C + 5D + 5E + 5F = 1500.
Разделив обе стороны уравнения на 5, мы получаем:
A + B + C + D + E + F = 300.
Однако шестое взвешивание в таблице показывает, что A + B + C + D + E = 300 фунтам. Следовательно, ящик F должен весить 0 фунтов. Обратимся затем к пятому взвешиванию, которое показывает, что A + B + C + D + F = 280 фунтам. Однако мы уже знаем, что F = 0, а значит A + B + C + D = 280.
Вернемся к шестому взвешиванию — A + B + C + D + E = 300, вычтем из него последнее уравнение и получим E = 20фунтов.
Из четвертого взвешивания следует, что A + B + C + E + F = 260. Подставив в это уравнение уже известные значения F и E, мы получим A + B + C + 20 + 0 = 260, или A + B + C = 240. Подставляя это значение в пятое взвешивание, находим D = 40.
Если вычесть уравнение третьего взвешивания из уравнения четвертого взвешивания, то, зная, что F = 0, мы получаем:
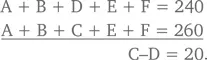
Поскольку D = 40, мы получаем C = 60.
Подставим известные значения в уравнение первого взвешивания: B + C + D + E + F = 200 = B + 60 + 40 + 20 + 0. Таким образом, B = 80.
Поступив аналогичным образом с уравнением второго взвешивания, получим A = 100.
Использование табличной формы сделало данные более понятными и позволило решить задачу путем логических рассуждений.
Даны трехзначные числа, которые составлены исключительно из нечетных цифр. Чему равна сумма всех этих чисел?
Обычно при решении задачи такого типа начинают составлять список нечетных чисел в том или ином порядке, а потом долго складывают их.
Главное здесь — организовать числа логичным образом. Например, наш список может выглядеть так: 111 + 113 + 115 + 117 + 119 + 133 + 135 + 137 + 139 + … + 511 + 513 + 515 + 517 + 519 + … + 991 + 993 + 995 + 997 + 999. Поскольку всего пять цифр могут находиться в каждом из трех разрядов, существует 5 × 5 × 5 = 125 возможных чисел. Если подойти к делу организованно, то можно складывать эти числа парами: первое и последнее, второе и предпоследнее и т. д. Сумма каждой из этих пар равна 1110. В нашем списке пар 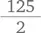 чисел. Таким образом, сумма этих чисел составляет
чисел. Таким образом, сумма этих чисел составляет 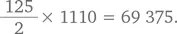
Читать дальше
Конец ознакомительного отрывка
Купить книгу



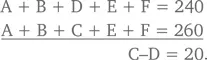
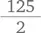 чисел. Таким образом, сумма этих чисел составляет
чисел. Таким образом, сумма этих чисел составляет