Альфред Позаментье - Стратегии решения математических задач. Различные подходы к типовым задачам

Даны два параллелограмма ABCD и APQR с точкой P на стороне BC и точкой D на стороне RQ , как показано на рис. 5.1. Если площадь параллелограмма ABCD 18, то чему равна площадь параллелограмма APQR ?

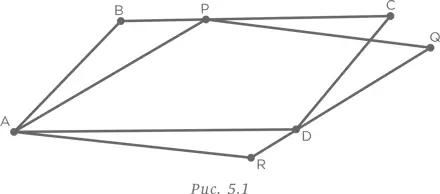
Эта задача не такая уж простая. Первая попытка решить ее заключается в поиске признаков конгруэнтности, означающих равенство площадей. Этот метод не дает результата. Более разумно, хотя и не слишком оригинально, провести линию PD , как показано на рис. 5.2.

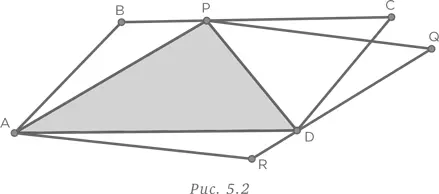
Теперь можно показать, что площадь треугольника APD составляет половину площади каждого из двух параллелограммов, поскольку в этот треугольник имеет общее основание с обеими параллелограммами и одинаковую высоту. Хотя это разумный подход к решению довольно сложной задачи, существует более изящный способ ее решения.

В условиях задачи просто говорится, что точка P лежит на стороне BC , но не указывается, где именно. Мы можем проанализировать экстремальную ситуацию. Можно, например, представить, что точка P совпадает с точкой B . Аналогичным образом можно представить, что точка D , лежащая на стороне RQ , совпадает с точкой R . В результате такого изменения, которое определенно соответствует исходным условиям задачи, два параллелограмма оказываются наложенными друг на друга и, следовательно, имеющими одну и ту же площадь. Таким образом, площадь параллелограмма APRQ равна 18.

Суммарное расстояние между съездами 1 и 20 на новой автомагистрали составляет 140 км. Между любыми двумя съездами должно быть не менее 7 км. Чему равно максимальное расстояние между любыми двумя соседними съездами?

Обычно пытаются подобрать различные комбинации чисел в надежде найти максимум. Существует, однако, более интересный подход.

Воспользуемся стратегией анализа экстремальных ситуаций. Прежде всего отметим, что между съездами 1 и 20 всего 19 «расстояний». Поскольку минимальное расстояние между любыми двумя съездами равно 7 км, рассмотрим экстремальную ситуацию, в которой все расстояния, кроме одного, равны 7 км. Тогда минимальная сумма 18 «расстояний» составит 18 × 7 = 126 км. Таким образом, максимальное расстояние между любыми двумя съездами равно 140–126 = 14 км, иначе не хватит километров, чтобы выдержать 7-километровую дистанцию между остальными съездами.

У нас есть две однолитровые бутылки. В одной — пол-литра красного вина, в другой — пол-литра белого. Мы берем столовую ложку красного вина, выливаем его в бутылку с белым вином и взбалтываем смесь. Затем мы берем столовую ложку полученной смеси (красного и белого вина) и выливаем ее в бутылку с красным вином.

Чего больше, красного вина в бутылке с белым вином или белого вина в бутылке с красным вином?

Существует несколько общепринятых подходов к решению такой задачи, в которых используют полученную из условий информацию, например о столовой ложке, которая может быть излишней. При определенном везении и сообразительности можно получить правильный ответ, однако это дело нелегкое, да и ответ нередко кажется неубедительным.

Понятно, что размер ложки не имеет реального значения, и что ложки могут быть как большими, так и маленькими. Допустим, мы используем очень большую столовую ложку, такую, которая вмещает пол-литра жидкости, — это будет экстремальная ситуация. После выливания пол-литра красного вина в бутылку с белым вином смесь будет состоять на 50 % из красного вина и на 50 % из белого. Перемешав смесь, мы берем пол-литровую ложку, наполняем ее и возвращаем смесь обратно в бутылку с красным вином. Смесь теперь одинакова в обеих бутылках. Это и есть наш ответ — красного вина в бутылке с белым вином столько же, сколько белого вина в бутылке с красным вином.

Найдите недостающие цифры в следующем семизначном числе, которое равно произведению трех последовательных чисел. Чему равны эти три числа? 1 2_ _ _ _6.