Альфред Позаментье - Стратегии решения математических задач. Различные подходы к типовым задачам

Решение этой задачи значительно упрощается при использовании стратегии анализа экстремальных ситуаций. Поместим точку P в экстремальную позицию так, чтобы она совпадала с точкой M или точкой A . Допустим, точка P совпадает с точкой A . Обратите внимание на то, что по мере смещения точки P вдоль BA в направлении точки A линия MD , которая должна оставаться параллельной PC , смещается так, что D приближается к средней точке линии BC . В конечном положении точки D линия AD становится медианой Δ ABC . Поскольку медиана делит треугольник на два треугольника с равными площадями, площадь Δ PBD равна половине площади Δ ABC .

Данное решение с помощью стратегии анализа экстремальных ситуаций ясно показывает важность отслеживания всех перемещений по мере смещения точки в предельное положение.

Два конгруэнтных квадрата, длина стороны которых равна 4 см, размещены так, что вершина одного из них находится в центре другого. Чему равно наименьшее значение площади пересекающейся части (рис. 5.6)?

Наиболее очевидный прием — построить два квадрата. Некоторые даже вычерчивают их в масштабе и пытаются измерить искомую площадь. Поскольку фигура получается неправильной, измерение ее площади может оказаться сложным.

Другой подход — провести несколько вспомогательных линий, например линии BM и CM . Несложно доказать, что два треугольника BSM и CTM конгруэнтны (конгруэнтность по двум углам и стороне) (см. рис. 5.7). Четырехугольник SCTM равен по площади треугольнику BCM , поскольку площадь треугольника добавляется к площади двух треугольников, которые, как мы доказали, являются конгруэнтными.

Поскольку ориентация квадратов не определена в условиях задачи, их можно разместить так, как нам захочется, лишь бы вершина одного находилась в центре другого. Обратимся к нашей стратегии анализа экстремальных ситуаций. Можно разместить квадраты так, как показано на рис. 5.8, где стороны этих фигур взаимно перпендикулярны.

Если этого недостаточно, чтобы удостовериться в равенстве закрашенной области четверти исходного квадрата, то нужно лишь продолжить линии PM и NM до пересечения со сторонами квадрата в точках J и K соответственно, как показано на рис. 5.9.

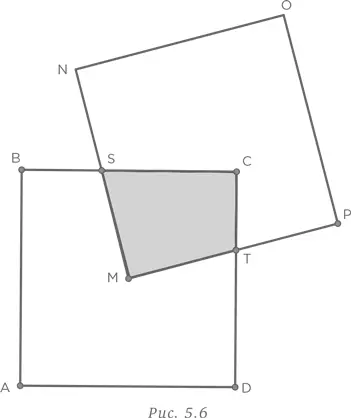
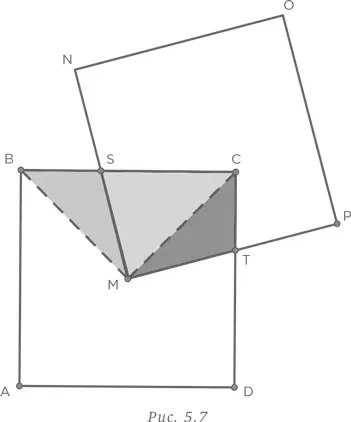
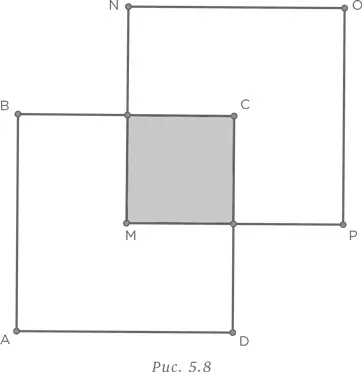
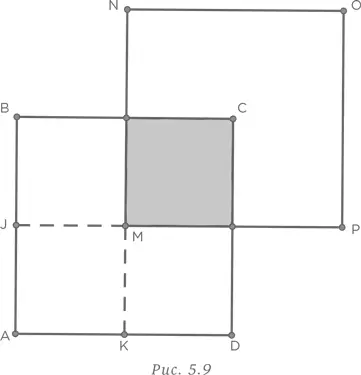
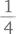Очевидно, что закрашенная область равна площади квадрата, или 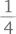части 16 см2, т. е. 4 см2. Разместив квадраты в определенном положении, мы легко нашли ответ.

Найдите значение x , которое удовлетворяет уравнению:

На первый взгляд задача кажется настолько ошеломляющей, что большинство людей не знают, как к ней подойти. И это не удивительно.

Посмотрим на это, как на своего рода экстремальную ситуацию. Начнем с того, что количество x в этом ряду бесконечно. Отбрасывание одной неизвестной x не должно никак влиять на результат в силу характера бесконечности. Таким образом, удалив первую неизвестную x , мы обнаружим, что все оставшиеся x так же должны быть равны 2. Это позволяет переписать уравнение, как x 2= 2. Следовательно x = ±√2. Если ограничиться положительными числами, то ответом будет x = √2.

Ниже показано, как с увеличением ряда значение приближается к 2.

Вот мы и нашли удивительно простое решение для очень сложной на первой взгляд задачи.