Dass der Angestellte Simplicio nicht erklärt, wie er auf den Betrag von 380 Florin gekommen ist, versteht sich fast von selbst: Simplicio ist ein leseunkundiger Bauer des 15. Jahrhunderts. Ein wenig addieren kann er, aber vom Multiplizieren hat er keine Ahnung. Deshalb rennt er ahnungslos in sein Unglück.
Die wichtigste Rechnung und das viele Geld
Wenn man bei 1,17 = 1,9487171 großzügig aufrundet, stimmt 1,17 etwa mit 2 überein. Dies bedeutet, dass sich bei einem Zinssatz von zehn Prozent im Verlauf von sieben Jahren die ursprüngliche Schuld fast verdoppelt. Wie ist das bei einem anderen Prozentsatz? Nehmen wir an, es wird Geld zu einem Jahreszins von zwei Prozent verliehen. Um festzustellen, nach wie vielen Jahren sich die Schuld verdoppelt haben wird, braucht man nur der Reihe nach die Potenzen von 1 + 2 % = 1 + 2/100 = 1 + 0,02 = 1,02 auszurechnen. Sie beginnen anfangs nur langsam zu wachsen: auf jeweils zwei Nachkommastellen gerundet
1,02 2 = 1,04, 1,02 3 = 1,06, 1,02 4 = 1,08, 1,02 5 = 1,10.
Diese Rechnungen zeigen: Nach fünf Jahren ist bei zwei Prozent Jahreszins die Schuld um zehn Prozent angewachsen. So viel, wie bei einem Jahreszins von zehn Prozent nach einem Jahr. Darum wird es bei einem Jahreszins von zwei Prozent fünfmal länger dauern, bis sich die Schuld verdoppelt hat, als bei einem Jahreszins von zehn Prozent. Mit anderen Worten: Bei einem Jahreszins von zwei Prozent wird sich nach fünf mal sieben, also nach 35 Jahren eine Verdopplung der Schuld ereignen. Tatsächlich zeigt die Rechnung mit dem Taschenrechner, dass 1,0235 = 1,999889552 …, also praktisch 2 ist. Und was für die Schulden gilt, gilt genauso für das Kapital, das man mit einem bestimmten Jahreszinssatz als Sparguthaben anlegt.
Die beiden genannten Zahlenbeispiele belegen eine Faustregel, die zu den wichtigsten Rechnungen zählt, welche die Mathematik der Menschheit geschenkt hat: Legt man ein Kapital zu einem bestimmten Prozentsatz Jahreszinsen an, braucht man nur die Zahl 70 durch die Zahl der Prozente zu dividieren, und man weiß, nach wie vielen Jahren sich das Kapital verdoppelt hat.9
Auf diese Verdopplung kommt es an. Denn wie bereits betont: Das Rechnen mit Prozenten beruht auf der Multiplikation.
Ein Beispiel: Angenommen, der heilige Josef, Marias Bräutigam, legt zu Christi Geburt für das kleine Jesuskind einen Euro bei der Bank von Bethlehem zum Zinssatz von 3,5 Prozent an. Dann hat sich nach 70 : 3,5, also nach 20 Jahren, der eine Euro zu zwei Euro verdoppelt. Nach 200 Jahren hat er sich zehnmal verdoppelt. Wegen 210 = 1024 also praktisch vertausendfacht: Aus einem Euro sind rund 1000 Euro geworden. Drei Nullen sind nach 200 Jahren an den einen Euro angehängt worden. Und heute, nach mehr als 2000 Jahren, sind zehn mal drei Nullen an den einen Euro angehängt worden. Jesu Erben könnten 1 000 000 000 000 000 000 000 000 000 000 Euro von der Bank von Bethlehem abholen. Eine Quintillion Euro. Das ist doch absurd!
Die Lösung des Rätsels besteht weniger darin, dass Jesus keine Erben hatte.
Die Lösung des Rätsels besteht schon eher, aber auch nicht ganz darin, dass die Bank von Bethlehem keine 2000 Jahre durchhält. Die Sieneser Bank „Monte di Pietá“ unserer Geschichte gibt es sogar noch heute: Sie wurde 1492 gegründet und 1624 in „Monte dei Paschi di Siena“ umbenannt. Es ist die älteste noch existierende Bank der Welt.
Die Lösung des Rätsels besteht vielmehr darin, dass es damals, zu Christi Geburt, keinen Euro gab, sondern Sesterzen. Eine Währung, die es heute nicht mehr gibt. Und Geld dazwischen, Taler, Florin, Gulden, gibt es heute auch nicht mehr. Kriege und Krisen, Inflationen und Währungsreformen vernichteten sie.
Wenn Zahlen ins Unvorstellbare anwachsen, werden sie auch für die Wirtschaft unzähmbar.
Donald Knuths Zahlenmonster
Mit der Erfindung der Potenzen steht der Mathematik ein Mittel zur Verfügung, Zahlen zu benennen, die selbst mit Multiplikationen, von Additionen ganz zu schweigen, kaum erreichbar sind. Denn man kann ja Potenzen noch einmal potenzieren und einen sogenannten „Potenzturm“ bilden, so zum Beispiel
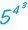 .
.
Allerdings ist hier darauf zu achten, dass es zwei Lesarten für diesen Potenzturm gibt. Eine Lesart besteht darin, dass man zuerst 54 berechnet, dies ist die Zahl 625, und dann von dieser die dritte Potenz, also 6253 = 244 140 625. In diesem Fall hat man den Potenzturm als
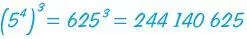
gelesen. Eine andere Lesart wäre, dass man zuerst 43 berechnet, dies ist die Zahl 64, und dann 5 zu dieser Potenz erhebt, also 564 ermittelt: Das ist ein Zahlenriese, der mit 5421 … beginnt und aus 45 Stellen besteht. In diesem Fall hat man den Potenzturm als
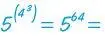

gelesen. Schreibt man einen Potenzturm ohne Klammern, einigt man sich darauf, immer die zweite der beiden genannten Lesarten zu meinen. Mit anderen Worten: Man „arbeitet“ den Potenzturm von rechts oben nach links unten „ab“. Diese Vereinbarung trifft man nicht nur deshalb, weil diese Lesart im Allgemeinen zu den viel größeren Zahlen führt, sondern vor allem darum, weil die andere Lesart den Potenzturm als solchen eigentlich gar nicht benötigt. Denn es ist zum Beispiel
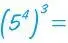 54 × 54 × 54 = 54 + 4 + 4 = 54 × 3,
54 × 54 × 54 = 54 + 4 + 4 = 54 × 3,
getreu dem Merkspruch aus der Schule: „Potenzen werden potenziert, indem man ihre Hochzahlen multipliziert.“
Die größte Zahl, die man bloß mit Hilfe von drei Ziffern schreiben kann, lautet demnach
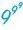 .
.
Es ist der aus drei Neunern bestehende Potenzturm. Dieser Zahlenriese beginnt mit 4281 … und hat 369 693 100 Stellen.
Der an der Stanford University lehrende Informatiker Donald E. Knuth ersetzte die von Bradwardine erfundene Potenzschreibweise durch eine neue Symbolik, die der einfachen Schrift, mit der Computer programmiert werden, besser angepasst ist: Statt 32 schrieb Knuth 3 ↑ 2. Der senkrechte Pfeil ersetzt gleichsam den Befehl, die nachkommende Zahl als Hochzahl zu schreiben. Damit, so entdeckte Knuth, kann man auch Potenztürme abkürzen: Es soll 3 ↑ ↑ 2 einen Potenzturm beschreiben, der aus zwei aufeinandergetürmten Zahlen 3 besteht. Das bedeutet: 3 ↑ ↑ 2 = 3 ↑ 3 = 33 = 27. Hier merkt man es noch nicht, aber dieser Doppelpfeil hat es in sich! Denn 3 ↑ ↑ 3 ist bereits der Potenzturm, der aus drei aufeinandergetürmten Zahlen 3 besteht, also
3 ↑ ↑3 = 3 ↑3 ↑3 =  = 327 = 7 625 597 484 987,
= 327 = 7 625 597 484 987,
und 3 ↑ ↑ 4 ist der Potenzturm, der aus vier aufeinandergetürmten Zahlen 3 besteht, also
3 ↑↑ 4 = 3 ↑3 ↑3 ↑3 = 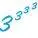 = 37 625 597 484 987.
= 37 625 597 484 987.
Dieser Zahlenriese beginnt mit 1258 … und hat 3 638 334 640 025 Stellen, ist also noch größer als der aus drei Neunern bestehende Potenzturm, den Knuth mit 9 ↑ ↑ 3 abkürzte.
Knuth baute seine Bezeichnung um einen weiteren Schritt aus: Setzte er zwischen zwei Zahlen einen Dreifachpfeil, so teilte die rechts vom Dreifachpfeil stehende Zahl mit, wie oft die links vom Dreifachpfeil stehende Zahl aufgeschrieben und dazwischen ein Doppelpfeil gesetzt wurde. Ausgewertet werden diese eigenartigen Objekte genauso wie die Potenztürme immer von rechts nach links. Es ist zum Beispiel 3 ↑ ↑ ↑ 2 die Abkürzung von 3 ↑ ↑ 3. Das ist die noch locker fassbare Zahl 7 625 597 484 987. Hingegen ist
Читать дальше

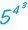 .
.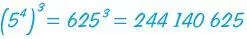
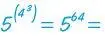

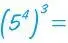 54 × 54 × 54 = 54 + 4 + 4 = 54 × 3,
54 × 54 × 54 = 54 + 4 + 4 = 54 × 3,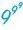 .
. = 327 = 7 625 597 484 987,
= 327 = 7 625 597 484 987,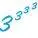 = 37 625 597 484 987.
= 37 625 597 484 987.










