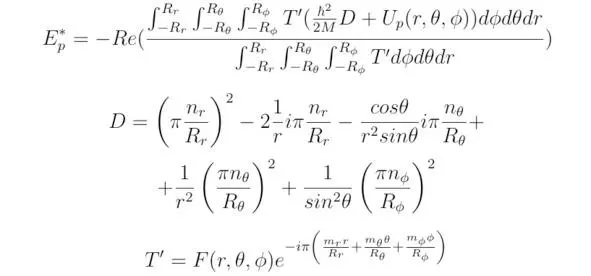Игорь Мерзляков - Квантовая химия в примерах

© Игорь А. Мерзляков, 2022

ISBN 978-5-4498-2768-5

Создано в интеллектуальной издательской системе Ridero

Теоретические принципы, положенные в основу данной работы, опираются на аналитическое решение уравнения Шрёдингера, которое было детально исследовано в первой книге серии «Путешествие в квантовую механику». Изучая положения по квантовой химии, читатель сможет разобраться в методике, позволяющей осуществить моделирование кристаллических структур, молекул и химических реакций.

Каждый принцип, связанный с предсказанием химических соединений, в этой работе выделен отдельно, поэтому хотелось бы надеяться на то, что данное обстоятельство поможет читателю быстрее освоить предлагаемый к изучению материал.

Со времён, когда жил и работал М. В. Ломоносов, кристаллография получила своё развитие благодаря учёным, формировавшим знания о ней как об отдельной науке. На сегодняшний день исследователи продолжают изучать симметрии в структурах химических веществ, пытаясь решить в общем виде задачу «компактной упаковки шаров», согласно которой шары (аналогично атомам в кристалле) помещаются в ящик, оставляя наименьшее свободное пространство. Цель подобных исследований состоит в том, чтобы выделить основные типы кристаллических структур. Часто для неоднородных структур остаётся открытым вопрос о диаметрах шаров и размерах упаковки, куда они помещаются, поскольку именно диаметр определяет вид атома, а линейные размеры упаковки дают информацию о будущих свойствах кристаллической решётки. Предлагаемая в книге методика является наиболее универсальной с вычислительной точки зрения по сравнению с другими численными алгоритмами поиска структур, вместе с тем результаты моделирования указывают на идентичность построенных теоретически и полученных на практике химических соединений.

В данной книге мы разберём основные методы, с помощью которых можно прогнозировать строение кристаллических структур и молекул, применяя аналитическое решение уравнения Шрёдингера, а также рассмотрим процессы возникновения и протекания химических реакций. Если химическую структуру возможно построить теоретически, тогда следует констатировать, что соответствующие ей кристалл или молекула будут существовать в природе. Смоделировав то или иное химическое соединение, необходимо определить параметры среды, в которых будет существовать исследуемое вещество на практике. В случае, когда нельзя обосновать теоретически структуру химического соединения, тогда вещество не может быть получено на практике даже в самых критических точках-параметрах среды, в которой оно находится.

Контакты для связи:vk.com/garrydipray, iganmer@gmail.com, iganmer@yandex.ru.

Ссылкана программу «Cepreak»: www.vk.com/cepreak

Из книги «Путешествие в квантовую механику» [1] известны следующие положения:

а) Полную энергию E электрона, определяемую для заданных квантовых чисел n x, n y, n z в трёхмерной декартовой системе координат, можно выразить в виде тождества:

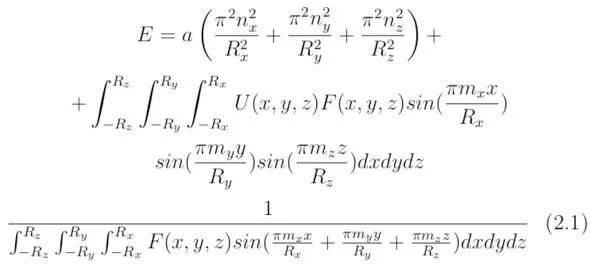
где x,y,z – координаты точек, куда помещается пробный отрицательный заряд (см. раздел 5 [1]), x∈ (-R x, R x), y∈ (-R y, R y), z∈ (-R z, R z), F (x,y,z) – произвольно заданная функция, U (x,y,z) – потенциальная энергия, R x, R y, R z – коэффициенты, определяемые из граничных условий. Величины m x/R x, m y/R y, m z /R z в общем случае будут зависеть от функции распределения внутренней энергии u, расположенной в пространстве потенциальных ям (см. раздел 9 «Принцип суперпозиции. Квантовая запутанность. Квантовый компьютер» [1]). Если квантовая система состоит из одной частицы, тогда коэффициент a можно определить из соотношения a=ħ 2/ (2M), здесь ħ – приведённая постоянная Планка, M – масса электрона, n x, n y, n z – величины, определяющие дискретные значения полной энергии.

б) Получим выражение для вычисления полной энергии квантовой системы, расположенной в произвольно заданном пространстве потенциальных ям. В рассматриваемом примере потребуем, чтобы синусоидальная функция, входящая в состав решения уравнения Шрёдингера, была построена в сферической системе координат (r,θ,φ), тогда:

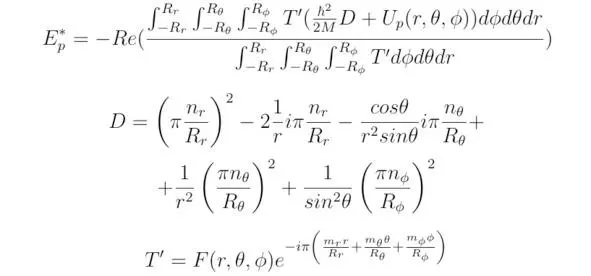
в) Распределение потенциальных ям в пространстве R 3 будет зависеть от значений синусоидальной функции A=sin (πm xx/R x) sin (πm yy/R y) sin (πm zz/R z). В точках, где величина A принимает отрицательные значения A <0, возможно обнаружить электроны, а в точках, где A> 0 – позитроны или ядра атомов.