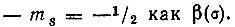Глава 2. Квантовомеханическое описание строений атома
В настоящей главе кратко изложены некоторые результаты квантовомеханической теории строения атома, причем основное внимание уделено тем ее аспектам, которые представляют интерес для теории химической связи.
Некоторые особенности квантовомеханического описания явлений микромира
В квантовой механике состояние N-электронной системы описывается волновой функцией 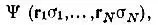 зависящей от пространственных координат (r i) и спиновых переменных (σ i) всех электронов. Эта функция должна удовлетворять уравнению Шредингера
зависящей от пространственных координат (r i) и спиновых переменных (σ i) всех электронов. Эта функция должна удовлетворять уравнению Шредингера
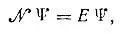 (2.1)
(2.1)
где 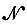 — оператор Гамильтона (гамильтониан), определяющий рассматриваемую систему и для атома с зарядом ядра Z,имеющий вид
— оператор Гамильтона (гамильтониан), определяющий рассматриваемую систему и для атома с зарядом ядра Z,имеющий вид
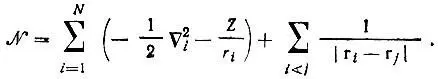 (2.2)
(2.2)
Не следует думать, что любое решение уравнения Шредингера (2.1) имеет физический смысл. В действительности на функцию Ψ накладываются определенные ограничения. В частности, для связанных состояний с дискретным спектром Е должно выполняться условие нормировки:
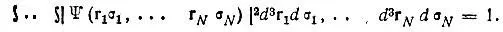 (2.3)
(2.3)
Для многоэлектронных систем чрезвычайно важным является требование антисимметричности волновой функции  относительно перестановок тождественных частиц (электронов):
относительно перестановок тождественных частиц (электронов):
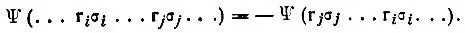 (2.4)
(2.4)
Одним из следствий этого требования, называемого принципом Паули, является то, что для трех и большего числа электронов основным состоянием не будет состояние с наименьшим собственным значением гамильтониана, так как последнему соответствует не имеющая физического смысла симметричная волновая функция.
Значение принципа Паули в теории химической связи исключительно велико, и мы в дальнейшем неоднократно будем к нему обращаться. Сейчас отметим только, что любую антисимметричную N-электронную функцию Ψ можно представить в виде линейной комбинации так называемых "детерминантов Слэтера", составленных из одноэлектронных волновых функций (спин-орбиталей):
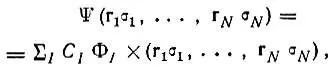 (2.5)
(2.5)
где
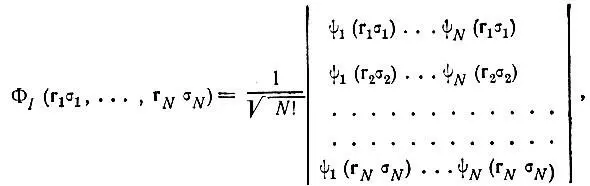 (2.6)
(2.6)
и индекс I при детерминанте Слэтера Φ Iобозначает определенную совокупность ортонормированных спин-орбиталей ψ i (rσ), которая называется спин-орбитальной конфигурацией.
В общем случае в разложение многоэлектронной волновой функции входит бесконечно много детерминантов Слэтера. Часто ограничивают это разложение одним или несколькими детерминантами. Качество такой аппроксимации зависит от качества включенных в Φ Iспин-орбиталей. Наилучшие спин-орбитали получаются в методе самосогласованного поля Хартри-Фока, на котором мы подробно остановимся в третьей главе.
Электронные конфигурации атомов, термы и тонкая структура энергетических уровней
Атомные спин-орбитали, описывающие одноэлектронные состояния в атоме, приближенно (без учета спин-орбитального взаимодействия) можно представить в виде произведения бесспиновой одноэлектронной волновой функции, называемой орбиталью, на одноэлектронную спиновую функцию, которая является собственной функцией оператора проекции собственного момента импульса электрона
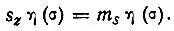 (2.7)
(2.7)
Собственные функции η(σ) , соответствующие положительному cобственному значению 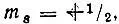 обозначаются как α(σ) , a отрицательному
обозначаются как α(σ) , a отрицательному 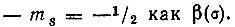
Читать дальше

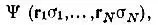 зависящей от пространственных координат (r i) и спиновых переменных (σ i) всех электронов. Эта функция должна удовлетворять уравнению Шредингера
зависящей от пространственных координат (r i) и спиновых переменных (σ i) всех электронов. Эта функция должна удовлетворять уравнению Шредингера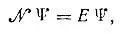 (2.1)
(2.1)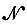 — оператор Гамильтона (гамильтониан), определяющий рассматриваемую систему и для атома с зарядом ядра Z,имеющий вид
— оператор Гамильтона (гамильтониан), определяющий рассматриваемую систему и для атома с зарядом ядра Z,имеющий вид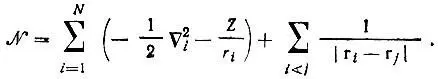 (2.2)
(2.2)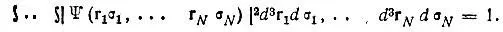 (2.3)
(2.3) относительно перестановок тождественных частиц (электронов):
относительно перестановок тождественных частиц (электронов):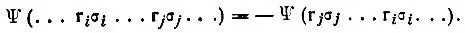 (2.4)
(2.4)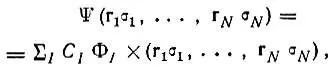 (2.5)
(2.5)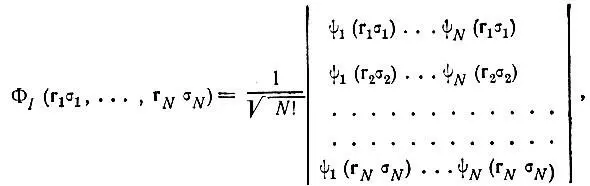 (2.6)
(2.6)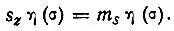 (2.7)
(2.7)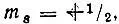 обозначаются как α(σ) , a отрицательному
обозначаются как α(σ) , a отрицательному