Перед Максвеллом и другими учеными того времени вставала проблема магнетиков (за них мы вскоре примемся). Они ничего не знали о циркулирующих токах, ответственных за атомный магнетизм и поэтому, в плотности тока утеряли еще одну часть. Вместо уравнения (32.16) они на самом деле писали

где Нотличается от e 0с 2 В, так как последнее учитывает эффекты атомных токов. (При этом j'представляет то, что осталось от токов.) Таким образом, у Максвелла было четыре полевых вектора: Е, D, Ви Н, причем в Dи Нскрывалось то, на что он не обратил внимания,— процессы, происходящие внутри вещества. Уравнения, написанные в таком виде, вы встретите во многих местах.
Чтобы решить их, необходимо как-то связать Dи Нс другими полями, поэтому зачастую писали
D =eE
и
В=mH.(32.18)
Однако эти связи верны лишь приближенно для некоторых веществ, и то лишь когда поля не изменяются слишком быстро со временем. (Для синусоидально изменяющихся полей зачастую можно писать уравнения таким способом, считая при этом e и m комплексными функциями частоты, но для произвольных изменений поля со временем это неверно.) На какие только ухищрения не пускаются ученые, чтобы решить уравнения! А мне кажется, что правильнее всего оставить уравнения записанными через фундаментальные величины, как мы понимаем их теперь, т. е. как раз то, что мы и проделали.
§ 3. Волны в диэлектрике
Теперь нам предстоит выяснить, какого сорта электромагнитные волны могут существовать в диэлектрическом веществе, где других зарядов, кроме тех, что связаны в атомах,
нет. Таким образом, мы возьмем r=-С· Ри j= д P/ д t . При этом уравнения Максвелла примут такой вид:
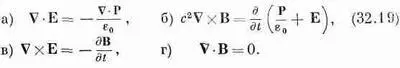
Мы можем решить эти уравнения, как делали это прежде. Начнем с применения к уравнению (32.19в) операции ротора:
СX(СX E)=-( д / д t)СX B.
Используя затем векторное тождество
СX(СX E) = С(С· E)-С 2 Eи подставляя выражение для СX Bиз (32.19б), получаем

Используя уравнение (32.19а) для С· Е, находим
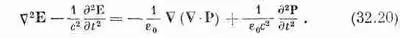
Таким образом, вместо волнового уравнения мы теперь получили, что даламбертиан Еравен двум членам, содержащим поляризацию Р.
Однако Рзависит от Е, поэтому уравнение (32.20) все еще допускает волновые решения. Сейчас мы будем ограничиваться изотропными диэлектриками, т. е. Рвсегда будет иметь то же направление, что и Е. Попробуем найти решение для волны, движущейся в направлении оси z. Электрическое поле при этом будет изменяться как е i( w t - kz ). Предположим также, что волна поляризована в направлении оси х, т. е. что электрическое поле имеет только x-компоненту. Все это записывается следующим образом:
E x=E 0e i ( w t - kz ). (32.21)
Вы знаете, что любая функция от (z- vt) представляет волну, бегущую со скоростью v. Показатель экспоненты в выражении (32.21) можно переписать в виде
-ik[z-(w/k)t],
так что выражение (32.21) представляет волну, фазовая скорость которой равна
v фаз=w/k.
В гл. 31 (вып. 3) показатель преломления n определялся нами из формулы
v фаз=c/n.
С учетом этой формулы (32.21) приобретает вид
Ex=E 0 e i w ( t - nz / c ) .
Таким образом, показатель n можно определить, если мы найдем ту величину k, которая необходима, чтобы выражение (32.21) удовлетворяло соответствующим уравнениям поля, и затем воспользуемся соотношением
n=kc/w. (32.22)
В изотропном материале поляризация будет иметь только x-компоненту; кроме того, Рне изменяется с изменением координаты х, поэтому С· P=0 и мы сразу же избавляемся от первого члена в правой стороне уравнения (32.20). Вдобавок мы считаем наш диэлектрик «линейным», поэтому Р х будет изменяться как е i w t и d 2 P x /dt 2 = -w 2P x. Лапласиан же в уравнении (32.20) превращается просто в д 2 E x /dz 2 =-k2Е x , так что в результате получаем
Читать дальше


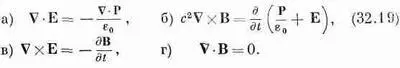

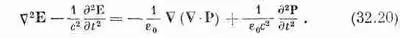



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
