§ 2. Уравнения Максвелла в диэлектрике
Наличие в веществе поляризации означает, что там возникают поляризационные заряды и токи, которые необходимо учитывать в полных уравнениях Максвелла при нахождении полей. Сейчас мы собираемся решать уравнения Максвелла для случая, когда заряды и токи не равны нулю, но неявно определяются вектором поляризации. Нашим первым шагом должно быть явное нахождение плотности зарядов r и плотности тока j,усредненных по тому же самому малому объему, который имелся в виду при определении вектора Р. Потом необходимые нам значения r и j могут быть определены из поляризации. В гл. 10 (вып. 5) мы видели, что когда поляризация Рменяется от точки к точке, то возникает плотность зарядов:
r пол=-С· Р. (32.9)
В то время мы имели дело со статическими полями, но эта же формула справедлива и для переменных полей. Но когда Ризменяется со временем, заряды движутся, так что появляется поляризационный ток. Каждый из осциллирующих зарядов вносит в ток свой вклад, равный произведению его заряда q e на скорость v. Когда же таких зарядов в единице объема N штук, то они создают плотность тока j:
j =Nq e v .
Ну а поскольку известно, что v=dx/dt, то j=Nq e dx/dt, что как раз
равно dP/dt.Следовательно, при переменной поляризации возникает плотность тока
j пол =d P/dt (32.10)
Наша задача стала теперь простой и понятной. Мы пишем уравнения Максвелла с плотностями заряда и тока, определяемыми поляризацией Рпосредством уравнений (32.9) и (32.10). (Предполагается, что других зарядов и токов в веществе нет.) Затем мы свяжем Рс Еформулой (32.5) и будем разрешать их относительно Еи В, отыскивая при этом волновое решение.
Но прежде чем приступить к решению, мне бы хотелось сделать одно замечание исторического характера. Первоначально Максвелл писал свои уравнения в форме, отличающейся от той, в которой они используются нами. И именно потому, что уравнения писались в другой форме в течение многих лет (да и сейчас многими пишутся так), я постараюсь объяснить вам разницу. В те дни механизм диэлектрической проницаемости не был понятен с ясностью и полнотой. Не была ясна ни природа атомов, ни существование поляризации в веществе. Поэтому тогда не понимали, что С· Pдает дополнительный вклад в плотность заряда р. Были известны только заряды, не связанные в атомах (такие, как заряды, текущие по проводу или возникающие при трении).
Сегодня же мы предпочитаем обозначать через r полную плотность зарядов, включая в нее и заряды, связанные с индивидуальными атомами. Если назвать эту часть зарядов r пол, то можно написать
r=r пол+r др,
где r др— плотность зарядов, учтенная Максвеллом и относящаяся к другим зарядам, не связанным с определенными атомами. При этом мы бы написали
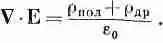
После подстановки r полиз (32.9) получаем
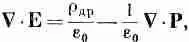
или

В плотность тока, фигурирующую в уравнениях Максвелла для СX B, вообще говоря, тоже вносится вклад от связанных атомных электронных токов. Поэтому мы можем написать
j= j пол+ j др,
причем уравнение Максвелла приобретает вид
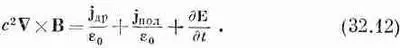
Используя уравнение (32.10), получаем
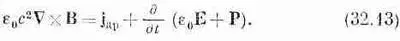
Теперь вы видите, что если бы мы определили новый вектор D
D=e 0 E+ P, (32.14)
то два уравнения поля приняли бы вид
С· D=r др(32.15)
и

Это и есть та форма уравнений, которую использовал Максвелл для диэлектриков. А вот и остальные два уравнения:
СX Е=- д B/ д t
и
С· B=0,
которые в точности совпадают с нашими.
Читать дальше

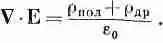
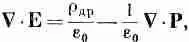

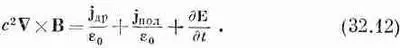
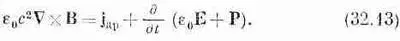




![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
