Я расскажу вам еще об одной теории, чтобы показать, до каких вещей додумываются люди, когда они увлечены. Это несколько другая модификация законов электродинамики, которую предложил Бопп.
Вы понимаете, что, решившись изменить уравнения электромагнетизма, можно делать это в любом месте. Вы можете изменить закон сил, действующих на электрон, или можете изменить уравнения Максвелла (как это будет сделано в теории, которую я собираюсь описать) или еще что-нибудь. Одна из возможностей — изменить формулы, определяющие потенциал через заряды и токи. Возьмем формулу, которая выражает потенциалы в некоторой точке через плотности токов (или зарядов) в любой другой точке в ранний момент времени. С помощью четырехвекторных обозначений для
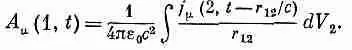
потенциалов мы можем записать ее в виде
(28.13)
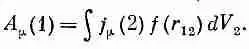
Удивительно простая идея Боппа заключается в следующем. Может быть, все зло происходит от множителя 1/r под интегралом. Предположим с самого начала, что потенциал в одной точке зависит от плотности зарядов в любой точке как некоторая функция расстояния между точками, скажем как f(r 12). Тогда полный потенциал в точке 1 будет определяться интегралом по всему пространству от произведения j mна эту функцию
Вот и все. Никаких дифференциальных уравнений, ничего больше. Есть только еще одно условие. Мы должны потребовать, чтобы результат был релятивистски инвариантным. Так что в качестве «расстояния» мы должны взять инвариантное «расстояние» между двумя точками в пространстве-времени. Квадрат этого расстояния (с точностью до знака, который несуществен) равен
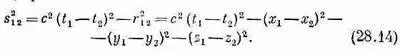
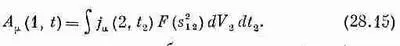
Так что для релятивистской инвариантности теории функция должна зависеть от s 12или, что то же самое, от s 2 12. Таким образом, в теории Боппа
(Интеграл, разумеется, должен браться по четырехмерному объему dt z dx z dy 2 dz 2 .)
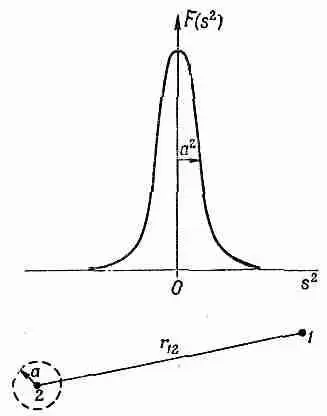
Фиг. 28,4. Функция F(s 2), используемая в нелокальной теории Боппа.
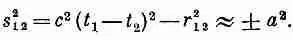
Теперь остается только выбрать подходящую функцию F. Относительно нее мы предполагаем только одно, что она повсюду мала, за исключением области аргумента вблизи нуля, т. е. что график F ведет себя подобно кривой, изображенной на фиг. 28.4. Это узкий пик в окрестности s 2=0, шириной которого грубо можно считать величину а 2. Если вычисляется потенциал в точке 1, то приближенно можно утверждать, что заметный вклад дают только те точки 2, для которых s 2 12= с 2(t 2-t 1 ) 2 -r 2 12отличается от нуля на ±a 2. Это можно выразить, сказав, что F важно только для
(28.16)
Если понадобится, можно проделать все математически более строго, но идея вам уже ясна.
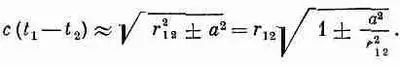
Предположим теперь, что а очень мало по сравнению с размерами обычных объектов типа электромоторов, генераторов и тому подобное, поэтому для обычных задач г 12>>а. Тогда выражение (28.16) говорит, что в интеграл (28.15) дают вклад только те токи, для которых t 1-t 2очень мало:
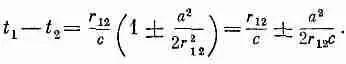
Но поскольку а 2/r 2 12<<1, то квадратный корень приближенно равен 1 ±а 2/2r 2 12, так что
В чем здесь суть? Полученный результат говорит, что для А m . в момент t 1 важны только те времена t 2, которые отличаются от него на запаздывание r 12/c с пренебрежимо малой поправкой, ибо r 1 2>>а. Другими словами, теория Боппа переходит в теорию Максвелла при удалении от зарядов в том смысле, что она приводит к эффекту запаздывания.
Читать дальше

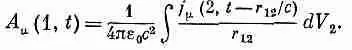
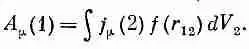
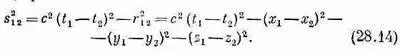
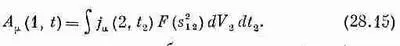

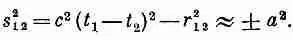
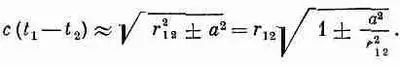
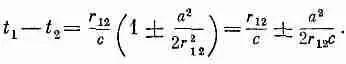



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
