[Если бы мы попытались решить (23.6а) старым прямолинейным способом, то оценили бы по достоинству магический «комплексный» метод.] Поделив обе части уравнения на exp(iwt), найдем отклик осциллятора 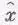 на силу
на силу 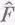
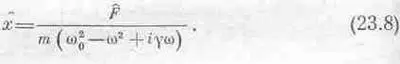
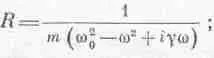
Итак, отклик x равен силе F, умноженной на некоторый множитель. Этот множитель не имеет ни названия, ни какой-то своей собственной буквы, и мы будем обозначать его буквой R:

тогда
Этот множитель можно записать либо как p+iq, либо как рехр(iq). Запишем его в виде рехр(iq) и посмотрим, к чему это приведет. Внешняя сила — это действительная часть числа F 0ехр(iD)ехр(iwt), она равна F 0 cos( w t +D). Уравнение (23.9) говорит нам, что отклик 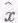 равен
равен 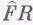 ; мы условились
; мы условились
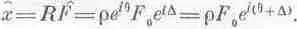
писать R в виде R=rехр(iq); следовательно,
Вспомним (об этом уже говорилось), что физическое значение х, равное действительной части комплексного числа х, равно действительной части rF 0exp[i(q+D)]exp(iwt). Но r и F 0 — действительны, а действительная часть ехр[i(q+D+wt)] — это просто cos(wt+D+q). Таким образом,
x=rF 0cos(wt+D+q). (23.10)
Это значит, что амплитуда отклика равна амплитуде силы F, умноженной на коэффициент усиления r; мы нашли «размах» колебаний. Но это еще не все: видно, что х колеблется не в такт с силой; фаза силы равна D, а у x; она сдвинута на дополнительную величину q. Следовательно, r и q — это величина и фазовый сдвиг отклика.
Найдем теперь значение r. Квадрат модуля любого комплексного числа равен произведению этого числа на комплексно сопряженное, т. е.
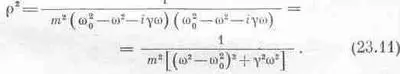
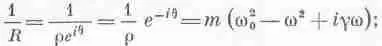
Можно найти и фазовый угол q

значит,
Знак минус возник оттого, что tg(-q) =-tgq. Угол q отрицателен при всех значениях w, т. е. смещение х отстает по фазе от силы F.
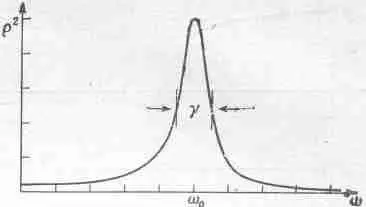
На фиг. 23.2 показано, как изменяется r 2при изменении частоты (r 2для физика интереснее, чем r, потому что r 2пропорционально квадрату амплитуды, а значит, и той энергии, которую передает осциллятору внешняя сила).
Фиг. 23.2. График зависимости r 2 от w .
Очевидно, что если g мало, то основной член в (23.11) — это 1/(w 2 0-w 2) 2, и отклик стремится к бесконечности, если w приближается к w 0. Но эта «бесконечность» — не настоящая бесконечность, потому что даже если w=w 0, то все еще остается слагаемое 1/g 2w 2. Зависимость сдвига фазы от частоты изображена на фиг. 23.3.
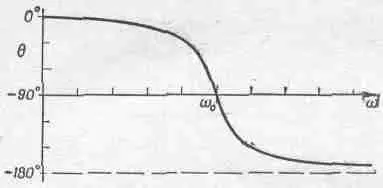
Фиг. 23.3. График зависимости q от w .
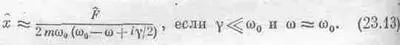
Иногда приходится иметь дело с формулой, немного отличающейся от (23.8); она тоже называется «резонансной» и, несмотря на некоторое отличие от (23.8), описывает те же самые явления. Дело в том, что если значение g очень мало, то наиболее интересная область резонансной кривой лежит около частоты w=w 0, а здесь при малых g формулу (23.8) с большой степенью точности можно заменить приближенной формулой. Поскольку w 2 0-w 2=(w 0-w)(w 0+w), то для w, очень близких к w 0, разность квадратов почти равна 2w 0(w 0-w), a gw можно заменить на gw 0. Значит, w 2 0-w 2+gw»2w 0(w 0-w+ig/2) и
Читать дальше

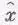 на силу
на силу 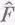
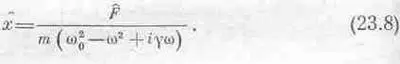
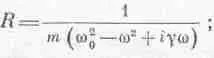

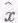 равен
равен 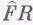 ; мы условились
; мы условились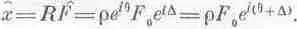
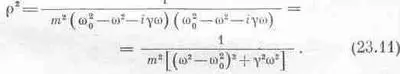
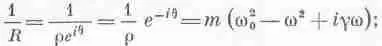



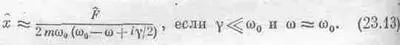



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)

