Ричард Фейнман - 2a. Пространство. Время. Движение

e it =cost+isint. (22.8)

Каковы свойства алгебраического косинуса cost и алгебраи­ческого синуса sin t? Прежде всего x 2 +y 2 =1; это мы уже до­казали, и это верно для любого основания, будь то 10 или е. Следовательно, cos 2t+sin 2t=l. Мы знаем, что e it =1+it для малых t; значит, если t — близкое к нулю число, то cos t близок к единице, a sin t близок к t. Продолжая дальше, мы придем к выводу, что все свойства этих замечательных функций, получаю­щихся в результате возведения в мнимую степень, в точности совпадают со свойствами тригонометрического синуса и триго­нометрического косинуса.

А как обстоит дело с периодом? Давайте найдем его. В ка­кую степень надо возвести е, чтобы получить i? Иными словами, чему равен логарифм i по основанию е? Мы вычислили уже ло­гарифм i по основанию 10; он равен 0,68226i; чтобы перейти к основанию е, мы умножим это число на 2,3025 и получим 1,5709. Это число можно назвать «алгебраическим p/2». Но по­глядите-ка, оно отличается от настоящего p/2 всего лишь послед­ним десятичным знаком, и это просто-напросто следствие на­ших приближений при вычислениях! Таким образом, чисто ал­гебраически возникли две новые функции — синус и косинус; они принадлежат алгебре и только алгебре. Мы пошли по их сле­дам и обнаружили, что это те же самые функции, которые так естественно возникают в геометрии. Мы отыскали мост между алгеброй и геометрией.

Подводя итог нашим поискам, мы напишем одну из самых замечательных формул математики

e i q=cosq+isinq. (22.9)

Вот она, наша жемчужина.

Связь между алгеброй и геометрией можно использовать для изображения комплексных чисел на плоскости; точка на плос­кости определяется координатами х и у (фиг. 22.2).

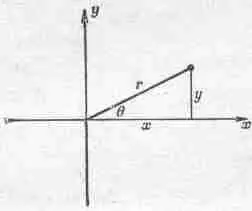
Фиг. 22.2. Комплексное число как точка на плоскости.

Представим каждое комплексное число в виде x+ iy. Если расстояние точки от начала координат обозначить через r, а угол радиуса-вектора точки с осью x — через q, то выражение x+iy можно представить в виде re i 9 . Это следует из геометрических соотношений между х, у, r и q. Таким образом, мы объединили алгебру и геометрию. Начиная эту главу, мы знали только целые числа и умели их считать. Зато у нас была небольшая идея о могуществе шага в сторону и обобщения. Используя алгебраические «законы», или свойства чисел, сведенные в уравнения (22.1), и определения обратных операций (22.2), мы смогли создать не только новые числа, но и такие полезные вещи, как таблицы логарифмов, степеней и тригонометрические функции (они возникли при возведении действительных чисел в мнимые степени), и все это удалось сделать, извлекая много раз квадратный корень из десяти!

* Квадратный корень лучше всего извлекать не тем способом, кото­рому обычно учат в школе, а немного иначе. Чтобы извлечь квадратный корень из числа N, выберем достаточно близкое к ответу число а, вы­числим N/a и среднее а'= 1 / 2 [а+(N/а)]; это среднее будет новым числом а, новым приближением корня из N. Этот процесс очень быстро приводит к цели: число значащих цифр удваивается после каждого шага.

§ 1. Комплексные числа и гармоническое движение

§ 2. Вынужденные колебания с торможением

§ 3. Электрический резонанс

§ 4. Резонанс в природе

§ 1. Комплексные числа и гармоническое движение

Мы снова будем говорить в этой главе о гармоническом осцилляторе, особенно об ос­цилляторе, на который действует внешняя си­ла. Для анализа этих задач нужно развить новую технику. В предыдущей главе мы ввели понятие комплексного числа, которое состоит из действительной и мнимой частей и которое можно изобразить на графике. Действительная часть числа будет изображаться абсциссой, а мнимая — ординатой. Комплексное число а можно записать в виде a=a r +ia i ; при такой записи индекс r отмечает действительную часть а, а индекс i — мнимую. Взглянув на фиг. 23.1, легко сообразить, что комплексное число a=x+iy можно записать и так: x+iy=rexp(i q ), где r 2 =x 2 +y 2 =(x+iy)(x-iy)=aa * (а* — это комплексно сопряженное к а число; оно полу­чается из а изменением знака i).