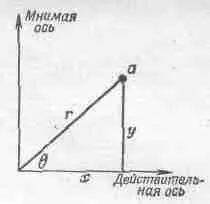
Фиг. 23,1. Комплексное число, изображенное точкой на «комплексной плоскости».
Итак, комплексное число можно представить двумя способами: явно выделить его действительную и мнимую части или задать его модулем r и фазовым углом q. Если заданы r и q, то х и у равны rcosq и rsinq, и, наоборот, исходя из числа x+iy, можно найти r=Ц(x 2 +y 2 ) и угол q; tgq равен у/х (т. е. отношению мнимой и действительной частей).
Чтобы применить комплексные числа к решению физических задач, проделаем такой трюк. Когда мы изучали осциллятор, то имели дело с внешней силой, пропорциональной coswt. Такую силу F=F 0 cos w t можно рассматривать как действительную часть комплексного числа F = F 0exp(iwt), потому что exp(iwt)=coswt+isinwt. Такой переход удобен: ведь иметь дело с экспонентой легче, чем с косинусом. Итак, трюк состоит в том, что все относящиеся к осциллятору функции рассматриваются как действительные части каких-то комплексных функций. Найденное нами комплексное число F, разумеется, не настоящая сила, ибо физика не знает комплексных сил: все силы имеют только действительную часть, а мнимой части взяться просто неоткуда. Тем не менее мы будем говорить «сила» F 0 exp(iwt), хотя надо помнить, что речь идет лишь о действительной ее части.
Рассмотрим еще один пример. Как представить косинусоидальную волну, фаза которой сдвинулась на D? Конечно, как действительную часть F 0 exp[i((wt-D 2)]; экспоненту в этом случае можно записать в виде exp[i( w t- D )]=ехр(i w t)exp( -i D ). Алгебра экспонент гораздо легче алгебры синусов и косинусов; вот почему удобно использовать комплексные числа. Часто мы будем писать так:

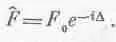
Шляпка над буквой будет указывать, что мы имеем дело с комплексным числом, т. е.
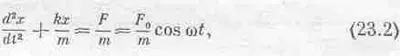
Однако пора начать решать уравнения, используя комплексные числа, тогда мы увидим, как надо применять комплексные числа в реальных обстоятельствах. Для начала попытаемся решить уравнение
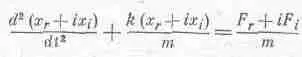
где F — действующая на осциллятор сила, а х — его смещение. Хотя это и абсурдно, предположим, что х и F — комплексные числа. Тогда х состоит из действительной части и умноженной на i мнимой части; то же самое касается и F. Уравнение (23.2) в этом случае означает
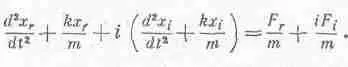
или
Комплексные числа равны, когда равны их действительные и мнимые части; следовательно, действительная, часть х удовлетворяет уравнению, в правой части которого стоит действительная часть силы. Оговорим с самого начала, что такое разделение действительных и мнимых частей возможно не всегда, а только в случае линейных уравнений, т. е. уравнений, содержащих х лишь в нулевой и первой степенях. Например, если бы уравнение содержало член l х 2 , то, сделав подстановку x r +ix t , мы получили бы l (x r +ix i ) 2 , и выделение действительной и мнимой частей привело бы нас к l (х 2 r -x 2 i) и 2ilx rx i. Итак, мы видим, что действительная часть уравнения содержит в этом случае член -l x 2 i . Мы получили совсем не то уравнение, какое собирались решать.
Попытаемся применить наш метод к уже решенной задаче о вынужденных колебаниях осциллятора, т. е. об осцилляторе, на который действует внешняя сила. Как и раньше, мы хотим решить уравнение (23.2), но давайте начнем с уравнения

где 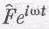 — комплексное число. Конечно, х — тоже комплексное число, но запомним правило: чтобы найти интересующие нас величины, надо взять действительную часть х. Найдем решение (23.3), описывающее вынужденные колебания. О других решениях поговорим потом. Это решение имеет ту же частоту, что и внешняя (приложенная) сила. Колебание, кроме того, характеризуется амплитудой и фазой, поэтому если представить смещение числом
— комплексное число. Конечно, х — тоже комплексное число, но запомним правило: чтобы найти интересующие нас величины, надо взять действительную часть х. Найдем решение (23.3), описывающее вынужденные колебания. О других решениях поговорим потом. Это решение имеет ту же частоту, что и внешняя (приложенная) сила. Колебание, кроме того, характеризуется амплитудой и фазой, поэтому если представить смещение числом  , то модуль его скажет нам о размахе колебаний, а фаза комплексного числа — о временной задержке колебания. Воспользуемся теперь замечательным свойством экспоненты:
, то модуль его скажет нам о размахе колебаний, а фаза комплексного числа — о временной задержке колебания. Воспользуемся теперь замечательным свойством экспоненты: 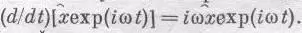
Читать дальше



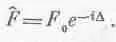
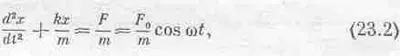
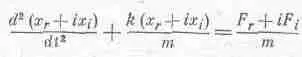
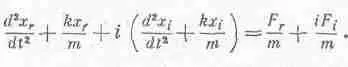

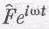 — комплексное число. Конечно, х — тоже комплексное число, но запомним правило: чтобы найти интересующие нас величины, надо взять действительную часть х. Найдем решение (23.3), описывающее вынужденные колебания. О других решениях поговорим потом. Это решение имеет ту же частоту, что и внешняя (приложенная) сила. Колебание, кроме того, характеризуется амплитудой и фазой, поэтому если представить смещение числом
— комплексное число. Конечно, х — тоже комплексное число, но запомним правило: чтобы найти интересующие нас величины, надо взять действительную часть х. Найдем решение (23.3), описывающее вынужденные колебания. О других решениях поговорим потом. Это решение имеет ту же частоту, что и внешняя (приложенная) сила. Колебание, кроме того, характеризуется амплитудой и фазой, поэтому если представить смещение числом  , то модуль его скажет нам о размахе колебаний, а фаза комплексного числа — о временной задержке колебания. Воспользуемся теперь замечательным свойством экспоненты:
, то модуль его скажет нам о размахе колебаний, а фаза комплексного числа — о временной задержке колебания. Воспользуемся теперь замечательным свойством экспоненты: 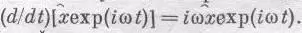



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)

