В этой теории природа происхождения совершенно беспорядочных движений молекул приписывалась очень частому столкновению молекул между собой. При столкновениях они обмениваются энергией, и молекулы в основном имеют энергии, близкие к среднему значению, одинаковому для всех молекул (тепловой энергии). Легко понять, что молекулы воздуха при комнатной температуре действительно должны двигаться совершенно хаотично. В 1 л воздуха содержится n = N А/22,4 л 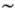 3·10 22молекул ( N А— постоянная Авогадро). Их средняя скорость v равна
3·10 22молекул ( N А— постоянная Авогадро). Их средняя скорость v равна 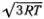 (где R — газовая постоянная), т. е. около 200 км/ч! Среднее расстояние l , которое молекула пробегает без столкновений, легко оценить с помощью соображений размерности. Оно очевидно зависит от размера молекул d и от числа молекул в единице объема и равно примерно l
(где R — газовая постоянная), т. е. около 200 км/ч! Среднее расстояние l , которое молекула пробегает без столкновений, легко оценить с помощью соображений размерности. Оно очевидно зависит от размера молекул d и от числа молекул в единице объема и равно примерно l  1/( d 2 n ), т. е. l
1/( d 2 n ), т. е. l  10 -5см. Поэтому в 1 с молекула испытывает примерно v / l
10 -5см. Поэтому в 1 с молекула испытывает примерно v / l  10 10столкновений!
10 10столкновений!
В таких условиях, конечно, нет никакого смысла следить за движением отдельной молекулы. Все они находятся в равном положении, можно говорить лишь об их средней скорости и средней энергии, которые и определяют давление и температуру газа. Что, однако, произойдет, если уменьшать число молекул в единице объема или понижать температуру? Столкновения будут становиться все реже и реже, а в конце концов движение может потерять неупорядоченный характер.
До какого предела движение останется хаотическим и можно пользоваться для описания его состояния такими усредненными характеристиками, как давление и температура? Ни Максвелл, ни Больцман не знали ответа на этот вопрос, да и сейчас, сто лет спустя, мы не умеем на него ответить. Возможно, что на столь общий вопрос и нет единственного ответа. Естественно попробовать сузить вопрос.
Что происходит при понижении температуры? При достаточно низкой температуре газ превратится в твердое тело. Рассмотрим поэтому движение частиц в кристалле. Сделаем еще одно упрощение и возьмем одномерный кристалл, который мы привыкли заменять моделью грузиков, связанных пружинками. Вот тут-то и выявляется в совершенно обнаженном виде самая суть вопроса. При достаточно низкой температуре грузики (молекулы) колеблются около своих положений равновесия, и беспорядок выражается в том, что фазы их колебаний распределены совершенно хаотически. Амплитуды колебаний и максимальные скорости также должны беспорядочно изменяться, но в среднем они должны быть одинаковы для каждого грузика. Возможен ли такой молекулярный беспорядок в модели грузиков?
Ответ на это, на первый взгляд, отрицательный. Вспомним линейную теорию движений грузиков, с которыми мы познакомились в гл. 4. Мы выяснили, что все движения системы из N грузиков представляют собой сумму N мод. Если бы при этом вначале была одна гармоника с частотой 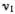 , то через время Т 1= 1/
, то через время Т 1= 1/ 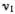 наша система возвратилась бы в начальное состояние.
наша система возвратилась бы в начальное состояние.
Если возбуждены все N независимых мод, то такое возвращение произойдет за время Т N = 1/ 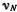 , где
, где 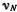 — минимальная частота...
— минимальная частота...
Ч и т а т е л ь. Постойте! А не нужно ли нам учесть трение?
А в т о р. Вы забыли, что мы имеем дело с молекулами, а не с реальными грузиками и пружинками! С молекулярной точки зрения, трение — это просто перераспределение энергии — переход энергии упорядоченного движения в энергию хаотического теплового движения. Если пренебречь внутренней структурой молекул и их взаимодействием с окружающей средой, то ни о каком трении говорить нельзя.
Ч и т а т е л ь. Я, может быть, неточно выразился. Я хотел сказать, что модель, в которой моды не зависят друг от друга, лишь приближенная. На самом деле они как-то связаны друг с другом?
А в т о р. Конечно, связаны, и естественно предположить, что взаимодействие одной гармоники с остальными будет приводить к потере ею энергии, т. е. действовать подобно трению. Тогда упорядоченное движение одной гармоники будет переходить в хаотическое движение остальных.
Итак, независимость мод связана с линейностью сил, связывающих грузики. Если нарушить линейность (скажем, пружины не подчиняются закону Гука), то можно ожидать, что движения грузиков станут хаотичными, по крайней мере в том случае, когда число грузиков N достаточно велико. Примерно так думало большинство физиков, в том числе и Энрико Ферми. Впрочем, возможно, что у Ферми были кое-какие сомнения на этот счет. Вероятно, его интересовало также, сколь большим должно быть число N . Достаточно ли велико N = 100 или же надо взять N = 1 000 000? *) К сожалению, Ферми не успел получить ответа на этот вопрос. Так или иначе, но первый серьезный вопрос, который он решил задать ЭВМ, был вопрос об установлении теплового равновесия в цепочке грузиков и нелинейных пружин. Результат машинного эксперимента оказался совершенно неожиданным.
Читать дальше

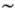 3·10 22молекул ( N А— постоянная Авогадро). Их средняя скорость v равна
3·10 22молекул ( N А— постоянная Авогадро). Их средняя скорость v равна 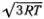 (где R — газовая постоянная), т. е. около 200 км/ч! Среднее расстояние l , которое молекула пробегает без столкновений, легко оценить с помощью соображений размерности. Оно очевидно зависит от размера молекул d и от числа молекул в единице объема и равно примерно l
(где R — газовая постоянная), т. е. около 200 км/ч! Среднее расстояние l , которое молекула пробегает без столкновений, легко оценить с помощью соображений размерности. Оно очевидно зависит от размера молекул d и от числа молекул в единице объема и равно примерно l  1/( d 2 n ), т. е. l
1/( d 2 n ), т. е. l 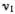 , то через время Т 1= 1/
, то через время Т 1= 1/ 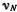 , где
, где 










