Напрасно в годы хаоса искать конца благого...
Б. Пастернак
О, дум заснувших не буди!
Поди ними хаос шевелится.
Ф. Тютчев
Мы, люди XX в., не любим беспорядка, и слово «хаос» для нас почти ругательное. Примерно такой смысл вкладывает в него Борис Пастернак. Поэт же прошлого века, Федор Иванович Тютчев, вкладывает в это слово совсем иной смысл. Чуть раньше он называет его «древним» и «родимым». Он, конечно, имеет в виду хаос древних греков — некое первичное состояние мира, все порождающее и все поглощающее, или «первоматерию». На современном языке такой хаос больше всего похож на состояние нашей Вселенной в первые мгновения после «Большого взрыва». Одна из глубоких проблем современной космологии — понять, как из этого хаотического состояния образовалась современная упорядоченная Вселенная с ее галактиками и звездами. На некоторых этапах развития вселенной солитоны, видимо, помогали ей упорядочиваться. Мы уже вскользь упоминали об этом, когда познакомились со спиральными рукавами галактик.
Другой тип беспорядочного движения хорошо известен каждому из наблюдений над течением воды. Проще всего увидеть рождение хаотического движения воды, если двигать какой-нибудь предмет плохо обтекаемой формы. Уже при небольшой скорости движения возникают вихри. При очень большой скорости может возникнуть так называемый турбулентный след, подобный тому, который наблюдается за кормой быстро движущегося корабля. В области следа частицы воды движутся совершенно беспорядочно, хаотически. Такие движения жидкости впервые начали изучать Кельвин, Буссинеск, Рейнольдс и Рэлей. Термин «турбулентность» ввел в обиход Кельвин, произведя его от латинского «turbulentus» (беспокойный, беспорядочный). Первые опыты по изучению турбулентного движения воды в обыкновенных водопроводных трубах выполнил Рейнольдс в 1883 г.
Турбулентность — очень сложное явление, точнее, комплекс явлений. Наблюдается много разных типов турбулентности, по-разному беспорядочных. Простых же математических моделей турбулентных движений долго не удавалось найти. Такие модели появились лишь недавно, и в их изучении основную роль играют машинные эксперименты. Это не удивительно, так как турбулентность тоже тесно связана с нелинейностью, и к ней в полной мере относятся приведенные выше слова фон Неймана.
Если у вас есть простая вычислительная машинка, вы можете изучить самую простую модель турбулентного движения. Эта модель поразительно проста, и тем не менее она воспроизводит характерные черты очень сложных и широко распространенных явлений образования хаоса. Существует целый класс подобных моделей, на мы приведем здесь одну. Для ее изучения нужно знать три арифметических операции!
Представьте себе ученую «блоху», владеющую всеми тремя действиями арифметики и прыгающую не просто так, а по определенному закону. Если она в момент времени t n = n · Δ t ( n = 0, 1, 2, 3, ...) сидит в точке x n на оси x , то в следующий момент t n+ 1= ( n + 1 ) Δ t она перепрыгивает в точку x n+ 1= b - x n 2, где b — некоторое выбранное число, свое для каждой блохи (назовем ее, скажем, «постоянной блохи»). Пусть блоха начинает движение из некоторой точки отрезка -2 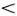 x
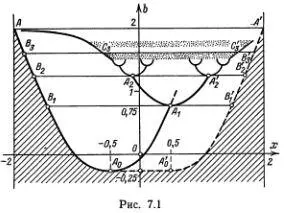
x 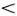 +2. Наша задача — определить, куда она может убежать за большое время, т. е. представить себе, каким может быть x n при больших значениях n .
+2. Наша задача — определить, куда она может убежать за большое время, т. е. представить себе, каким может быть x n при больших значениях n .
Как ни проста эта задача на вид, вам едва ли удастся найти ее решение без помощи микрокалькулятора. Однако прежде чем приступить к экспериментам, стоит немного подумать, чего от них можно ожидать. Рассмотрим кривую AA 0 A 1(рис. 7.1), соответствующую уравнению x 2+ x = b . Если x n стремится к некоторому пределу, то предельное значение будет лежать на этой кривой.
Численные эксперименты, однако, показывают, что только блохи, для которых точки с координатами ( x 0, b ) лежат внутри фигуры A 0 B 1 B 1' A 0' (кривая A 0' A 0получается зеркальным отражением относительно оси Ob ), приближаются к кривой A 0 А 1. При этом на ветвь A 0 A они никогда не попадают, а если их постоянные b и начальные координаты x 0таковы, что точка ( x 0, b ) лежит в заштрихованной области, то такие блохи убегают на бесконечность. Судьба наших ученых блох с постоянной b 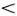 0,75 полностью определена. Что бы они ни делали, они либо погибают «в бесконечности», либо притягиваются к точкам на кривой A 0 А 1, где мы их легко ловим. Почти столь же печальна судьба блох, у которых ( x 0, b ) лежит в области B 1 B 2 B 2' B 1'. Они в конце концов попадают на кривую A 2 A 1 A 2', и при достаточно большом n перескакивают на каждом шаге с A 1 A 2' на A 1 A 2и обратно. Уравнение этой кривой тоже легко определить, воспользовавшись тем, что в пределе больших n после двух последовательных скачков, блоха оказывается вблизи той же ветви, т. е. x 2+ n
0,75 полностью определена. Что бы они ни делали, они либо погибают «в бесконечности», либо притягиваются к точкам на кривой A 0 А 1, где мы их легко ловим. Почти столь же печальна судьба блох, у которых ( x 0, b ) лежит в области B 1 B 2 B 2' B 1'. Они в конце концов попадают на кривую A 2 A 1 A 2', и при достаточно большом n перескакивают на каждом шаге с A 1 A 2' на A 1 A 2и обратно. Уравнение этой кривой тоже легко определить, воспользовавшись тем, что в пределе больших n после двух последовательных скачков, блоха оказывается вблизи той же ветви, т. е. x 2+ n  x n . Отсюда находим x n+ 2= b - ( b - x n 2) 2и в пределе, когда x n+ 2
x n . Отсюда находим x n+ 2= b - ( b - x n 2) 2и в пределе, когда x n+ 2  x n
x n  x , находим для x уравнение ( b - x 2) 2- ( b - x ) = 0. Легко проверить, что левая часть этого уравнения равна произведению двух множителей: ( x 2+ x - b ) и ( x 2 - x + 1 - b ). Обращение в нуль первого множителя дает кривую AA 0 A 1, а второго — кривую A 2 A 1 A 2'.
x , находим для x уравнение ( b - x 2) 2- ( b - x ) = 0. Легко проверить, что левая часть этого уравнения равна произведению двух множителей: ( x 2+ x - b ) и ( x 2 - x + 1 - b ). Обращение в нуль первого множителя дает кривую AA 0 A 1, а второго — кривую A 2 A 1 A 2'.
Читать дальше

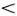 x
x 
 x n . Отсюда находим x n+ 2= b - ( b - x n 2) 2и в пределе, когда x n+ 2
x n . Отсюда находим x n+ 2= b - ( b - x n 2) 2и в пределе, когда x n+ 2 










