Работа, о которой мы собираемся рассказать, была сделана в лабораториях Лос-Аламоса, возникших в связи с атомным проектом. Впоследствии эти лаборатории стали также одним из главных центров изучения нелинейных явлений, в частности хаоса. Не случайно, что Фейгенбаум сделал свое открытие будучи сотрудником этих лабораторий. Даже самым оригинальным и независимым умам для работы необходима определенная атмосфера. Что такое эта «атмосфера», определить очень трудно, еще труднее ее создать. В Лос-Аламосе такая атмосфера была, и работа Фейгенбаума появилась не на пустом месте.
Но вернемся к задаче, поставленной Ферми перед ЭВМ. Вместе с математиками Станиславом Уламом и Джоном Пастой он в 1952 г. задумал выполнить обширные машинные эксперименты по исследованию нелинейных задач. Первой из них и была задача о порождении теплового хаоса в цепочке грузиков с нелинейными пружинками. Как вспоминал С. Улам: «Ферми часто говорил, что будущие фундаментальные физические теории будут, вероятно, основаны на нелинейных уравнениях, и поэтому было бы полезно попрактиковаться в математике, необходимой для понимания нелинейных систем. План состоял в том, чтобы начать с простейшей, по возможности, физической модели... затем постепенно увеличивать сложность и общность решаемых на машине задач... Решение всех этих задач послужило бы подготовкой к установлению, в конце концов, модели движений системы, в которой должны были бы наблюдаться «перемешивание» и «турбулентность»... За одно лето Ферми весьма быстро научился программировать задачи для ЭВМ и мог не только спланировать общую схему расчета, но и самостоятельно провести подробное программирование всей задачи. Результаты вычислений, проведенных на старой машине МАНИАК, оказались интересными и весьма неожиданными для Ферми. По его мнению, они явились некоторым откровением». Машина сумела настолько удивить Ферми, что он, уже будучи смертельно больным, интересовался продолжением расчетов и говорил, что эта одна из самых важных задач, с которыми он когда-либо встречался. Что же так поразило Ферми?
Ферми, Паста и Улам предложили машине рассчитать колебания системы из 32 грузиков, связанных пружинками, которые при растяжении их на Δ l создают возвращающую силу k Δ l + α (Δ l ) 2. При этом нелинейная поправка α (Δ l ) 2считалась малой по сравнению с основной, линейной силой k Δ l . Таким образом, машина должна была решать систему из 32 уравнений, подобных уравнениям (4.8), но с добавленными в правой части нелинейными силами α [( x i +1- x i ) 2- ( x i - x i- 1) 2]. Так как эти добавки малы, то можно следить не за движением отдельных частиц, а за изменением синусоидальных мод линейных уравнений, получающихся при α = 0. При α 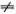 0 моды перестают быть независимыми, и энергия медленно (по сравнению с их периодами) перекачивается из одной моды в другую.
0 моды перестают быть независимыми, и энергия медленно (по сравнению с их периодами) перекачивается из одной моды в другую.
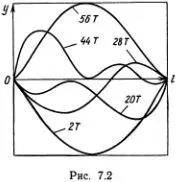
Рассмотрим движение из начального состояния, в котором возбуждена одна 1-я мода (обозначим ее период буквой Т ). Сначала действительно начинается перекачивание энергии в другие моды. Однако никакой хаотичности в этом не наблюдается (см. рис. 7.2). При t  20 Т возбуждена в основном 3-я мода. Затем начинает «солировать» 2-я мода (при t
20 Т возбуждена в основном 3-я мода. Затем начинает «солировать» 2-я мода (при t  28 Т ). При t
28 Т ). При t  44 Т энергия оказывается сосредоточена в 3-й моде, и при t
44 Т энергия оказывается сосредоточена в 3-й моде, и при t  56 Т снова возвращается к 1-й. Более высокие моды возбуждаются мало, максимальная энергия 4-й моды меньше половины энергии первой (т. е. полной энергии), а 5-я мода может получить не более шестой части полной энергии. На рис. 7.2 изображены вычисленные отклонения грузиков в различные моменты времени (масштаб по оси y для удобства сильно увеличен).
56 Т снова возвращается к 1-й. Более высокие моды возбуждаются мало, максимальная энергия 4-й моды меньше половины энергии первой (т. е. полной энергии), а 5-я мода может получить не более шестой части полной энергии. На рис. 7.2 изображены вычисленные отклонения грузиков в различные моменты времени (масштаб по оси y для удобства сильно увеличен).
Может быть, это случайность? Нет, при увеличении числа грузиков, при изменении α , при изменении самой формы нелинейной силы (скажем, β(Δ l ) 3вместо α (Δ l ) 2) это явление сохраняется. Моды не сливаются в общий беспорядочный хор, а выделяют несколько солистов, которые выступают по очереди, остальные им аккомпанируют. Когда возвращается первый солист, все начинается сначала! Время возвращения Т в(в нашем случае Т в  56 Т ) зависит от числа N , от вида нелинейности, но солирование низших мод и возвращение при Т = Т внаблюдалось всегда.
56 Т ) зависит от числа N , от вида нелинейности, но солирование низших мод и возвращение при Т = Т внаблюдалось всегда.
Читать дальше

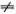 0 моды перестают быть независимыми, и энергия медленно (по сравнению с их периодами) перекачивается из одной моды в другую.
0 моды перестают быть независимыми, и энергия медленно (по сравнению с их периодами) перекачивается из одной моды в другую.
 20 Т возбуждена в основном 3-я мода. Затем начинает «солировать» 2-я мода (при t
20 Т возбуждена в основном 3-я мода. Затем начинает «солировать» 2-я мода (при t 










