В гл. 5 мы уже сравнивали дисперсию длинных волн на мелкой воде и в цепочке упруго связанных атомов (формулы (5.21) и (5.17)) и убедились, что зависимость фазовой скорости от λ имеет при больших значениях λ один и тот же вид. Достаточно заменить h на 1/2α, где α — расстояние между атомами, и из закона дисперсии волн на воде получится закон дисперсии длинных волн в цепочке атомов. Зная этот удивительный факт, совсем не трудно додуматься и до того, что в других физических системах закон дисперсии длинных волн может быть таким же. Однако такая мысль многие десятилетия никому не приходила в голову. Может быть, это произошло потому, что волнами на воде и в кристаллах интересовались разные исследователи, может быть, по другим причинам... Во всяком случае, ясная идея о существовании такого универсального закона дисперсии длинных волн сформировалась совсем недавно, уже в эпоху общего увлечения солитонами.
Чтобы теперь понять — как устроены волны КдФ, нужно ввести простейшую мыслимую нелинейность. Мы знаем, что скорость линейных диспергирующих волн не зависит от амплитуды, а зависит лишь от длины волны. Скорость же распространения нелинейных волн зависит и от амплитуды. Самая простая зависимость — линейная, когда рост скорости прямо пропорционален увеличению амплитуды. Именно она и реализуется для волн КдФ, а будучи самой простой, естественно, встречается и во многих других физических системах. Забуски и Крускал обнаружили, что такая нелинейность хорошо описывает нелинейные взаимодействия атомов в решетке. Еще раньше, в 1958 г., советский физик Р. З. Сагдеев подметил аналогию между некоторыми волнами в плазме и волнами на мелкой воде и показал, что в плазме также могут распространяться уединенные волны. Плазмой в это время уже занимались многие физики, и это наблюдение не осталось незамеченным. Вскоре удалось показать, что эти волны в плазме также можно описывать с помощью КдФ-уравнения. Это решило судьбу КдФ-уравнения, которое было извлечено из забвения и стало известно широкому кругу физиков и математиков. Знаменитым оно стало после того, как 3абуски и Крускал выяснили, что оно описывает солитоны, которые не изменяются после столкновения друг с другом, и что можно найти его самое общее решение. Это удалось в 1967 г. американским ученым Гарднеру, Грину, Крускалу и Миуре. От их работы обычно отсчитывают начало бурного развития науки о солитонах.
Выглядит уравнение КдФ совсем не страшно. Форма волны y ( t, х ) в момент времени t должна подчиняться соотношению
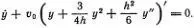
Здесь точкой обозначена производная по времени при фиксированном значении координаты х , а штрихом — производная по координате в заданный момент времени t . Если нарисовать зависимость профиля волны у от координаты, то этот график будет двигаться и деформироваться с течением времени. При этом у определяет наклон касательной к графику в точке х в момент t , а 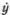 — скорость движения точки графика у ( t, х ) по направлению оси у . Если в некоторый момент времени t нам известна зависимость у от х (в том числе и производные у' , y'' , у''' ), то уравнение позволяет найти скорости
— скорость движения точки графика у ( t, х ) по направлению оси у . Если в некоторый момент времени t нам известна зависимость у от х (в том числе и производные у' , y'' , у''' ), то уравнение позволяет найти скорости 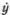 всех точек графика, так что можно приближенно определить его вид в следующий момент t + Δ t :
всех точек графика, так что можно приближенно определить его вид в следующий момент t + Δ t :
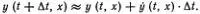
Решить такое уравнение — значит по начальному графику у (0, х ) найти вид графика y ( t, х ) в любой последующий момент времени. Точное решение этой очень непростой математической задачи оказалось одним из наиболее замечательных достижений математики, которое стало возможным благодаря тесному и плодотворному сотрудничеству физиков, математиков и использованию ЭВМ.
Нетрудно понять, что КдФ-уравнение описывает лишь волны, распространяющиеся в одном направлении вдоль оси х . Заметим сначала, что эффекты дисперсии определяются членом 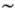 у" , а нелинейные эффекты — членом
у" , а нелинейные эффекты — членом 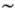 у 2. Если ими пренебречь, то получится совсем простое уравнение
у 2. Если ими пренебречь, то получится совсем простое уравнение 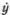 + v 0 y' = 0, которое мы обсуждали в гл. 5. Как оказалось, самое общее решение этого уравнения — любая функция от х - v 0 t , т. е. у ( t, х ) = f (х - v 0 t ). Чтобы найти зависимость у от х в любой момент времени, достаточно нарисовать график функции у = f ( х ) и двигать его со скоростью v 0( v 0
+ v 0 y' = 0, которое мы обсуждали в гл. 5. Как оказалось, самое общее решение этого уравнения — любая функция от х - v 0 t , т. е. у ( t, х ) = f (х - v 0 t ). Чтобы найти зависимость у от х в любой момент времени, достаточно нарисовать график функции у = f ( х ) и двигать его со скоростью v 0( v 0 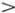 0) в положительном направлении оси х. Чтобы описать волну, бегущую в противоположном направлении, нужно взять другой знак перед v 0.
0) в положительном направлении оси х. Чтобы описать волну, бегущую в противоположном направлении, нужно взять другой знак перед v 0.
Читать дальше

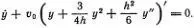
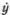 — скорость движения точки графика у ( t, х ) по направлению оси у . Если в некоторый момент времени t нам известна зависимость у от х (в том числе и производные у' , y'' , у''' ), то уравнение позволяет найти скорости
— скорость движения точки графика у ( t, х ) по направлению оси у . Если в некоторый момент времени t нам известна зависимость у от х (в том числе и производные у' , y'' , у''' ), то уравнение позволяет найти скорости 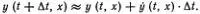
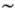 у" , а нелинейные эффекты — членом
у" , а нелинейные эффекты — членом 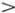 0) в положительном направлении оси х. Чтобы описать волну, бегущую в противоположном направлении, нужно взять другой знак перед v 0.
0) в положительном направлении оси х. Чтобы описать волну, бегущую в противоположном направлении, нужно взять другой знак перед v 0.










