На самом деле уравнение (6.12) было известно уже в прошлом веке и называлось уравнением струны в упругой среде (действие упругой среды на каждый кусочек струны описывается членом 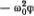 в правой части уравнения). Уравнение (6.11) также встречалось математикам в конце прошлого века. Оно появилось в связи с исследованиями по геометрии Лобачевского *) и было известно лишь геометрам. Достаточно полное изучение решений уравнения (6.11) было выполнено лишь в 1936 г. немецким математиком Р. Штойервальдом. Он нашел решения, соответствующие (на нашем с вами языке) одному солитону, двум солитонам и бризеру. Эти результаты до самого последнего времени были известны лишь немногим специалистам по геометрии и не оказали никакого влияния на развитие науки о солитонах. Для физики уравнение «синус-Гордона» было открыто Френкелем и Конторовой, и они же нашли его солитонное решение. Связать эти открытия с их именами естественно и справедливо, хотя наиболее удивительные свойства модели ФК были обнаружены позднее другими исследователями. Как сказал Больцман: «Еще почти никогда... не бывало, чтобы та самая голова, которая впервые натолкнулась на ту или иную новую идею, до конца исчерпала бы ее».
в правой части уравнения). Уравнение (6.11) также встречалось математикам в конце прошлого века. Оно появилось в связи с исследованиями по геометрии Лобачевского *) и было известно лишь геометрам. Достаточно полное изучение решений уравнения (6.11) было выполнено лишь в 1936 г. немецким математиком Р. Штойервальдом. Он нашел решения, соответствующие (на нашем с вами языке) одному солитону, двум солитонам и бризеру. Эти результаты до самого последнего времени были известны лишь немногим специалистам по геометрии и не оказали никакого влияния на развитие науки о солитонах. Для физики уравнение «синус-Гордона» было открыто Френкелем и Конторовой, и они же нашли его солитонное решение. Связать эти открытия с их именами естественно и справедливо, хотя наиболее удивительные свойства модели ФК были обнаружены позднее другими исследователями. Как сказал Больцман: «Еще почти никогда... не бывало, чтобы та самая голова, которая впервые натолкнулась на ту или иную новую идею, до конца исчерпала бы ее».
*) Любому решению этого уравнения соответствует некоторая поверхность, на которой выполняются аксиомы геометрии Лобачевского. Такие реализации геометрии Лобачевского сыграли основную роль в признании его идей.
Что, наконец, представляется нам затверделым и плот-
ным, то состоять из начал крючковатых должно не-
сомненно, сцепленных между собой наподобие веток
сплетенных.
Тит Лукреций Кар
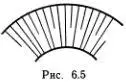
Всякий знает, что металлы сами по себе довольно «мягкие» или, лучше сказать, пластичные. Речь идет о «совершенном» металле, который имеет простую, не искаженную примесями и дефектами кристаллическую структуру. Кристаллическая решетка большинства металлов построена из одинаковых «кубиков». Вдоль плоскостей этих «кубиков» кристалл легко можно сдвинуть. Если вы сложите стопкой монеты, то небольшим боковым усилием легко сдвинете ее. Точно так же легко сдвигается по некоторым плоскостям идеальный кристалл. Такой сдвиг происходит совсем легко, если приложенное усилие создает дислокации, которые бегут одна за другой. Вам не нужно сдвигать сразу много атомов, а достаточно образовать дислокацию, для чего требуется небольшое усилие. По этой причине чистые, правильные кристаллы многих металлов очень мягкие. Однако бывает, что куски одной и той же на вид проволоки гнутся совсем не одинаково. Эти куски одинаковы лишь внешне, а внутренняя структура у них совсем разная. Те, которые гнутся плохо, подверглись обработке: вероятно, их уже сгибали. Возможно, вы замечали, что проволоку часто легче согнуть, чем разогнуть. А причина тому — дислокации. При сгибании в кристалле неизбежно образуется большое число дислокаций. Расстояния между атомами при этом практически не изменяются, но кристалл в одних направлениях растягивается, а в других — сжимается. Обратимся к рис. 6.5: линии изображают, конечно, довольно схематично, правильные ряды атомов кристалла, а их обрывы — это дислокации.
Если при сгибании образуется очень много дислокаций, они начинают «мешать» друг другу. Точнее говоря, кристалл становится настолько несовершенным, что дислокации по нему уже не смогут распространяться свободно. Если вспомнить модель, с которой мы начинали, то можно сказать, что правильно чередующиеся ямки становятся довольно нерегулярными.
Образуются широкие холмы и овраги, за которые дислокации «зацепляются». Чтобы разогнуть кристалл, вам приходится перемещать уже огромные коллективы атомов, а не «передислоцировать» их небольшие группки. Вот и выходит, что разогнуть совсем не то, что согнуть! Между прочим, то же самое — образование большого числа перепутанных дислокаций и других дефектов — происходит при ковке металлов. Можно сильно уменьшить число дислокаций, которые образовались при сгибании и разгибании проволоки, если «отжечь» проволоку. После отжига она снова станет совсем мягкой. Вы можете удивить своих менее просвещенных друзей простым фокусом — «я пятаки могу ломать». Прокалите достаточно толстую проволоку в огне газовой горелки. Остыв, она останется мягкой, и из нее легко можно сделать кольцо на палец или браслет на запястье, в зависимости от толщины проволоки. Предложите затем доверчивому зрителю разогнуть это кольцо!..
Читать дальше

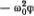 в правой части уравнения). Уравнение (6.11) также встречалось математикам в конце прошлого века. Оно появилось в связи с исследованиями по геометрии Лобачевского *) и было известно лишь геометрам. Достаточно полное изучение решений уравнения (6.11) было выполнено лишь в 1936 г. немецким математиком Р. Штойервальдом. Он нашел решения, соответствующие (на нашем с вами языке) одному солитону, двум солитонам и бризеру. Эти результаты до самого последнего времени были известны лишь немногим специалистам по геометрии и не оказали никакого влияния на развитие науки о солитонах. Для физики уравнение «синус-Гордона» было открыто Френкелем и Конторовой, и они же нашли его солитонное решение. Связать эти открытия с их именами естественно и справедливо, хотя наиболее удивительные свойства модели ФК были обнаружены позднее другими исследователями. Как сказал Больцман: «Еще почти никогда... не бывало, чтобы та самая голова, которая впервые натолкнулась на ту или иную новую идею, до конца исчерпала бы ее».
в правой части уравнения). Уравнение (6.11) также встречалось математикам в конце прошлого века. Оно появилось в связи с исследованиями по геометрии Лобачевского *) и было известно лишь геометрам. Достаточно полное изучение решений уравнения (6.11) было выполнено лишь в 1936 г. немецким математиком Р. Штойервальдом. Он нашел решения, соответствующие (на нашем с вами языке) одному солитону, двум солитонам и бризеру. Эти результаты до самого последнего времени были известны лишь немногим специалистам по геометрии и не оказали никакого влияния на развитие науки о солитонах. Для физики уравнение «синус-Гордона» было открыто Френкелем и Конторовой, и они же нашли его солитонное решение. Связать эти открытия с их именами естественно и справедливо, хотя наиболее удивительные свойства модели ФК были обнаружены позднее другими исследователями. Как сказал Больцман: «Еще почти никогда... не бывало, чтобы та самая голова, которая впервые натолкнулась на ту или иную новую идею, до конца исчерпала бы ее».











