Александр Филиппов - Многоликий солитон

Более совершенный «генератор солитонов», основанный на том же принципе, можно сделать из гвоздей и пружин. Основная идея должна быть понятна из рис. 6.7.

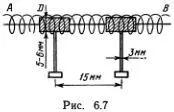
Маятники насаживаются на хорошо натянутую фортепианную струну диаметром 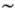1 мм. Необходимо, чтобы трение при вращении держателя D на струне было как можно меньше. В приборе, который был построен в 1969 г. А. Скоттом (примерные параметры его и приведены на рис. 6.7), длина солитона была 5 см, а v 0 50 см/с. На своем приборе А. Скотт наблюдал столкновения солитона с солитоном и антисолитоном, зависимость размера солитона от скорости, дисперсию волн и другие закономерности и явления.

В общем, частная и в какой-то степени общественная жизнь солитонов вполне доступна наблюдению невооруженным глазом. Ясно, что она была столь же доступна наблюдению и в 1869 г. Только, как мы знаем, она тогда никого не интересовала. Общая идея солитона родилась в наше время, и солитон — дитя середины ХХ в. Нам пора вернуться в него, но сначала надо сказать еще несколько слов о «ручном» солитоне и о некоторых других солитонах, похожих на солитоны Френкеля.

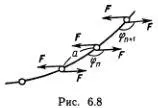
Покоящийся «ручной» солитон, или солитон Эйлера, тоже описывается, как уже говорилось в гл. 3, уравнением маятника. Только роль времени играет длина дуги. Показать это совсем не сложно, если взять дискретную модель проволоки, сделанную из твердых стерженьков, соединенных пружинными шарнирами (вспомните, как устроены бельевые прищепки). Рассмотрим несколько секций этой модели проволоки, изображенных на рис. 6.8. Проволока растягивается силой F . Применяя третий закон Ньютона к каждому стерженьку длины α , легко понять, что на него действует пара сил F , момент которой равен Fα sin φ n. Пружинные шарниры стремятся выпрямить «проволочку». Полный закручивающий момент, действующий на n -й стерженек, можно представить в виде К (φ n +1- 2φ n + φ n -1). Равновесие устанавливается, если этот момент равен нулю. Переходя, как обычно, к пределу непрерывной проволочки, т. е. считая длину стерженька малой, получим уравнение маятника

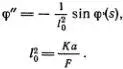
Здесь, как всегда, функция φ( s ) получена переходом φ n → φ( nα ) → φ( s ), штрихи обозначают дифференцирование по длине дуги s .

Величина l 0имеет размерность длины, так как [ К ] = [ F ] · [ L ]. Как мы сейчас увидим, l 0— это размер ручного солитона. Предполагается, конечно, что при уменьшении α жесткость пружин возрастает так, чтобы величина Кα оставалась конечной.

Форма солитона описывается хорошо знакомым выражением

φ( s ) = π - 4 arctg (е - s / l 0).

На первый взгляд кажется, что нарисовать эту кривую не так-то просто. Действительно, здесь s — длина дуги, а φ( s ) — угол наклона касательной к оси х , так что совсем неясно, как изобразить реальную кривую у ( х ), а не график зависимости φ от s . Оказывается, однако, что можно довольно просто построить кривую у ( х ) по точкам, пользуясь лишь циркулем и линейкой. Это построение изображено на рис. 6.9. Основано оно на том, что точка кривой Эйлера, имеющая на ней «координату» s , лежит на окружности в плоскости ( х , у ) с радиусом 2 l 0и центром на оси х с координатой s . Математически это можно записать следующим образом:

[ х ( s ) - s )] 2+ [ у ( s )] 2= 4 l 0 2.

Если найдена, скажем, точка А 2, лежащая на окружности с радиусом l 0и центром в точке — 2 α , то для отыскания точки А 3построим окружность с центром в точке — 3 α ( α — малая длина) и найдем точку пересечения с ней малой окружности радиуса α с центром в точке А 2, которая и оказывается точкой А 3. Точно так же строятся остальные точки А 4, А 5, ... Чем меньше Δ s = α , тем ближе будет построенная по точкам ломаная кривая к гладкой кривой Эйлера.

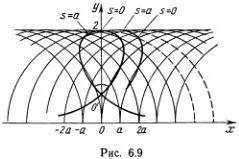
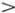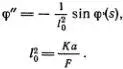
Если построение выполнено достаточно точно, угол самопересечения кривой будет равен примерно 110°. На рис. 6.9 мы взяли l 0= 1. От l 0зависит не форма, а лишь общий размер кривой, так как все они подобны. Солитон с размером l 0 1 получается увеличением всех размеров нарисованного солитона в l 0раз (преобразование подобия, или «фотоувеличение»). Это замечательное свойство ручного солитона легко увидеть на опыте. Если же угол сильно отклоняется от 110° или заметно меняется при уменьшении размера петли, когда вы увеличиваете силу натяжения F , ваша проволочка не годится для наблюдения солитона, надо подыскать другую.