Упражнение : выполните построение рис. 6.4. Покажите, что координаты точки А 1подчиняются соотношению (6.9), координаты точки С 1равны ω 0/ω 1и u 1/ v 0= v 0/ v 1, где ω 1— значение ω, соответствующее заданному значению λ = λ 1.
Полученный нами закон дисперсии очень часто встречается в самых разных физических явлениях, и стоит потратить некоторое время, чтобы как следует понять его. Особенно полезно представить его с помощью дисперсионной формулы
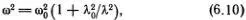
которая легко получается заменой в формуле (6.9) отношения v / v 0на (λω/λ 0ω 0).
Отсюда сразу видно замечательное свойство этого закона дисперсии — частота распространяющихся по цепочке волн всегда выше частоты ω 0, с которой колебался бы каждый атом цепочки вблизи своего положения равновесия, если бы он находился только под действием «подкладки». Физически очевидно, что частота ω 0достигается при очень большой длине волны, когда соседние атомы смещаются без изменения относительно расстояния (как твердое тело). При этом пружины настолько слабо деформируются, что их как бы и нет.
Другое свойство закона дисперсии (6.9) роднит его с гравитационными волнами на глубокой воде. Мы видим, что фазовая скорость v (λ) увеличивается с увеличением длины волны. Правда, эта зависимость несколько иная — скорость очень длинных волн на воде пропорциональна 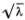 , а скорость волн смещения пропорциональна λ (при λ
, а скорость волн смещения пропорциональна λ (при λ 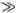 λ 0). Тем не менее можно считать, что природа прохождения дисперсии в обоих случаях качественно сходна. Во всяком случае, найденная нами дисперсия волн смещения в атомной цепочке не связана с ее дискретной структурой, которая может проявиться лишь при очень малых длинах волн, порядка постоянной решетки α .
λ 0). Тем не менее можно считать, что природа прохождения дисперсии в обоих случаях качественно сходна. Во всяком случае, найденная нами дисперсия волн смещения в атомной цепочке не связана с ее дискретной структурой, которая может проявиться лишь при очень малых длинах волн, порядка постоянной решетки α .
При выводе закона дисперсии мы, в сущности, с самого начала пренебрегали дискретной структурой, предполагая, что α 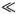 λ и α
λ и α 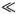 λ 0. Нетрудно проверить, что λ 0= 2π l 0(проверьте!). Поэтому при α
λ 0. Нетрудно проверить, что λ 0= 2π l 0(проверьте!). Поэтому при α 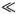 λ 0будет также выполнено условие α
λ 0будет также выполнено условие α 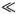 l 0, т. е. размер дислокации l 0должен быть большим по сравнению с межатомным расстоянием. Отсюда ясно, что дефект по Френкелю, размер которого примерно равен α , нельзя описать с помощью изложенной здесь теории. Если, однако, не гнаться за точностью, то можно считать дефект по Френкелю просто дислокацией малого размера l 0, сравнимого с α . Описание при этом будет качественно правильным.
l 0, т. е. размер дислокации l 0должен быть большим по сравнению с межатомным расстоянием. Отсюда ясно, что дефект по Френкелю, размер которого примерно равен α , нельзя описать с помощью изложенной здесь теории. Если, однако, не гнаться за точностью, то можно считать дефект по Френкелю просто дислокацией малого размера l 0, сравнимого с α . Описание при этом будет качественно правильным.
Если это не вполне понятно, нужно вспомнить начало предыдущей главы, где описаны колебания системы из двух и трех грузиков, соединенных пружинками. Эти колебания соответствуют стоячим волнам сплошной резинки (рис. 5.4 и 5.5), но только нельзя рассматривать волны с длиной, меньшей 2 α . Более точное описание дефекта по Френкелю можно найти с помощью исходного уравнения (6.1). Если пружины очень мягкие, т. е. если kα 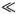 f 0, то существует равновесное состояние, в котором один из атомов смещен примерно на α , а все остальные смещены мало (попробуйте это проверить самостоятельно!). Это и есть дефект по Френкелю.
f 0, то существует равновесное состояние, в котором один из атомов смещен примерно на α , а все остальные смещены мало (попробуйте это проверить самостоятельно!). Это и есть дефект по Френкелю.
Раз уж мы вспомнили переход от цепочки атомов к сплошной среде, стоит написать, во что превратится при таком переходе основное уравнение (6.1). Как и при выводе уравнения Д'Аламбера, можно считать, что второй член в правой части перейдет в kα 2 y" . Переходя от y ( t , х ) к φ( t , х ) (вспомните вывод уравнений (6.4), (6.5), найдем в результате, что

Если ω 0= 0, то из этого уравнения получается уравнение Д'Аламбера.
К уравнению (6.11) приклеилось странное название — уравнение «синус-Гордона» . Происхождение этого жаргонного наименования связано с тем, что при значениях φ, мало отличающихся от π, т. е. φ = π + ψ, где 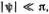 оно переходит в уравнение
оно переходит в уравнение

Это, а если говорить совсем точно, несколько более общее уравнение было предложено в 1926 г. Э. Шрёдингером, О. Клейном, В. Гордоном и В. А. Фоком, и обычно физики для краткости называют его уравнением Клейна — Гордона . Подобное стремление к укорочению названий породило и сочетание «синус-Гордона».
Читать дальше

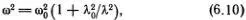
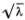 , а скорость волн смещения пропорциональна λ (при λ
, а скорость волн смещения пропорциональна λ (при λ 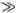 λ 0). Тем не менее можно считать, что природа прохождения дисперсии в обоих случаях качественно сходна. Во всяком случае, найденная нами дисперсия волн смещения в атомной цепочке не связана с ее дискретной структурой, которая может проявиться лишь при очень малых длинах волн, порядка постоянной решетки α .
λ 0). Тем не менее можно считать, что природа прохождения дисперсии в обоих случаях качественно сходна. Во всяком случае, найденная нами дисперсия волн смещения в атомной цепочке не связана с ее дискретной структурой, которая может проявиться лишь при очень малых длинах волн, порядка постоянной решетки α .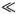 λ и α
λ и α 
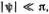 оно переходит в уравнение
оно переходит в уравнение











