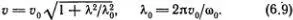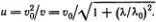
в ней стоит скорость звука v 0. Эту аналогию с теорией относительности можно провести достаточно далеко. Можно показать, что энергия Е и импульс р движущейся дислокации также выражаются формулами «теории относительности»
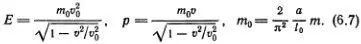
Таким образом, быстро движущиеся дислокации подчиняются не механике Ньютона, а механике специальной теории относительности. При малой скорости движения дислокации ( v 2/ v 0 2 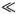 1) можно пользоваться обычной нерелятивистской теорией.
1) можно пользоваться обычной нерелятивистской теорией.
Эта модель, вероятно, очень понравилась бы Джозефу Лармору (1857—1942), считавшему частицы чем-то вроде дислокаций в эфире. Правда, его теория намного сложнее, но суть дела именно такая. С интересом отнесся бы к этой модели и Пуанкаре. В своем докладе «Новая механика» (1909 г.) он говорил: «Инерцией обладает не материя, а эфир; он один оказывает сопротивление движению, так что можно было бы сказать: нет материи, есть только дыры в эфире». В конце этой книги мы познакомимся с некоторыми современными идеями, связывающими элементарные частицы с солитонами некоторых нелинейных полей, играющих в какой-то степени роль эфира.
Во что превратились звуковые волны
Итак, мы уже поняли, что солитоны перемещаются со скоростями, меньшими v 0. А как же с обычными звуковыми волнами — могут ли они распространяться в среде, смоделированной Френкелем и Конторовой?
Возвратимся к уравнению (6.2). Даже для волн очень малой амплитуды его правую часть отбросить нельзя. Можно только приближенно заменить ее на -2π f 0( y n / α ). Тогда сразу видно, что y n ( t ) будет изменяться по синусоидальному закону, если величина «эффективной массы» m • отрицательна. При положительной эффективной массе никаких колебаний y n ( t ) не получится (вспомните гл. 4!). Предположим поэтому, что m • 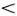 0. Тогда из формулы (6.3) следует, что скорость распространения волны v должна быть больше v 0, т. е. больше чем в свободной цепочке атомов! Не противоречит ли это только что сделанным вычислениям? Конечно, нет. Скорость v — это фазовая скорость волны, и мы сейчас увидим, что скорость группы волн оказывается всегда меньше v 0.
0. Тогда из формулы (6.3) следует, что скорость распространения волны v должна быть больше v 0, т. е. больше чем в свободной цепочке атомов! Не противоречит ли это только что сделанным вычислениям? Конечно, нет. Скорость v — это фазовая скорость волны, и мы сейчас увидим, что скорость группы волн оказывается всегда меньше v 0.
Итак, подставим в формулу (6.2) соотношение (6.3) и заменим sin [2π ( y n / α )] на 2π ( y n / α ). Для у n ( t ) получаем тогда уравнение малых (линейных) колебаний
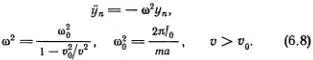
Решения этого уравнения, например
у n ( t ) = у n ( t n ) соs [ω( t - t n )],
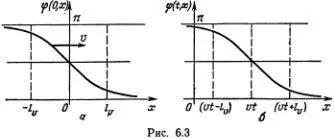
описывают, как и раньше, бегущие волны. Вспоминая рассуждения, приведенные при выводе формулы (6.5), представим волну смещения атомов в виде
у ( t , х ) = у 0соs [ω( t - x / v )].
Зависимость круговой частоты волны ω от фазовой скорости определяется формулой (6.8). Из условия связи длины волны с частотой и скоростью, т. е. из обычного соотношения λ = v / 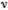 = 2π v /ω, легко находим зависимость фазовой скорости от длины волны:
= 2π v /ω, легко находим зависимость фазовой скорости от длины волны:
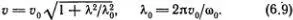
Упражнение : получите формулы (6.8), (6.9), воспользовавшись формулами (6.2), (6.3). Найдите групповую скорость и из формулы (5.23).
О т в е т: 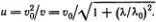
Зависимость скорости v от длины волны λ изображается хорошо изученной нами кривой — гиперболой. Обозначив v / v 0= X и λ/λ 0= Y , можно записать уравнение (6.9) в более знакомом и приятном виде как Y 2- Х 2= 1. Как мы уже убедились в гл.4, точки этой кривой можно находить с помощью циркуля и линейки. Это построение выполнено на рис. 6.4, где
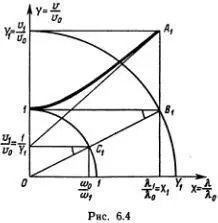
введены обозначения X 1 = λ 1/λ 0, Y 1= v 1/ v 0, 1/ Y 1= u 1/ v 0, λ 1— интересующее нас значение длины волны, v 1— соответствующее значение фазовой скорости, определяемое формулой (6.9), а u 1= v 0 2/ v 1— значение групповой скорости.
Читать дальше


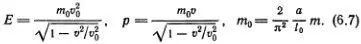
 1) можно пользоваться обычной нерелятивистской теорией.
1) можно пользоваться обычной нерелятивистской теорией. 0. Тогда из формулы (6.3) следует, что скорость распространения волны v должна быть больше v 0, т. е. больше чем в свободной цепочке атомов! Не противоречит ли это только что сделанным вычислениям? Конечно, нет. Скорость v — это фазовая скорость волны, и мы сейчас увидим, что скорость группы волн оказывается всегда меньше v 0.
0. Тогда из формулы (6.3) следует, что скорость распространения волны v должна быть больше v 0, т. е. больше чем в свободной цепочке атомов! Не противоречит ли это только что сделанным вычислениям? Конечно, нет. Скорость v — это фазовая скорость волны, и мы сейчас увидим, что скорость группы волн оказывается всегда меньше v 0.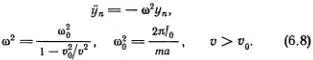
 = 2π v /ω, легко находим зависимость фазовой скорости от длины волны:
= 2π v /ω, легко находим зависимость фазовой скорости от длины волны: