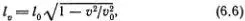Легко свести уравнение (6.2) к уравнению маятника (4.1). Вспомним, что sin (π + φ) = -sin φ, и положим 2π( y n / α ) = π + φ n , т. е. будем измерять отклонение атома от положения равновесия «углом» φ n . Если атом остался на месте, то y n = 0 и φ n = -π. Если он смещается вправо, то угол φ n возрастает и при y n = α принимает значение +π. Таким образом, переходу атома со дна одной «ямки» на дно другой соответствует асимптотическое движение «маятника». При таком изменении обозначений уравнение движения (6.2) можно записать в виде (проверьте это!)

Движение «маятника» по сепаратрисе, когда φ n ( t ) изменяется от -π до +π, мы уже определили раньше (вспомним формулу (4.9) и рис. 4.10). Напишем эту формулу еще раз:
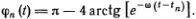
Так как маятники качаются с запаздыванием, мы выбрали свое начало отсчета времени t n для каждого из маятников. Поскольку смещение атомов от ячейки к ячейке распространяется со скоростью v = α/ Δ t , надо взять t n = n Δ t . Тогда φ 1( t ) = φ 0( t - Δ t ), и вообще φ n ( t ) = φ 0( t - n Δ t ).
Выразим теперь t n через скорость дислокации, т. е. t n = nα• (Δ t /α) = nα / v , и заменим nα на х . Будем писать соответственно φ n ( t ) = φ( t , х ), где х = nα . Тогда функцию φ( t , х ), описывающую движущуюся дислокацию, можно записать в виде
φ( t , х ) = π - 4 arctg [ e - ω( t - x/v )].
Эта функция определяет форму дислокации в любой момент времени:
y n ( t ) = α /2 + ( α /2π) φ ( t , nα ).
Удобно записать показатель экспоненты в форме ( х - vt )/ l v , где l v = v /ω. Вспоминая определения «частоты» ω и «массы» m •(см. формулы (6.4) и (6.3)), после простых преобразований получаем

В этом выражении для величины l 0под корнем написана безразмерная величина, равная отношению неких двух энергий. Выясним смысл этих энергий. Вспоминая, что v 0= 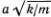 , представим mv 0 2как kα 2. Эта величина пропорциональна энергии, необходимой для растяжения пружины на величину порядка α . В знаменателе стоит произведение силы f 0на расстояние α , что, очевидно, пропорционально работе, которую надо затратить на преодоление барьера, отделяющего одну ямку от другой. Таким образом, l 0увеличивается при увеличении жесткости пружин и уменьшении силы со стороны «подкладки», привязывающей атомы к определенным местам. В дальнейшем будем считать, что упругая энергия kα 2значительно превосходит f 0 α , и, таким образом, величина l 0
, представим mv 0 2как kα 2. Эта величина пропорциональна энергии, необходимой для растяжения пружины на величину порядка α . В знаменателе стоит произведение силы f 0на расстояние α , что, очевидно, пропорционально работе, которую надо затратить на преодоление барьера, отделяющего одну ямку от другой. Таким образом, l 0увеличивается при увеличении жесткости пружин и уменьшении силы со стороны «подкладки», привязывающей атомы к определенным местам. В дальнейшем будем считать, что упругая энергия kα 2значительно превосходит f 0 α , и, таким образом, величина l 0 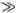 α .
α .
Теперь посмотрим на окончательное выражение для функции φ( t , х ), описывающей дислокацию
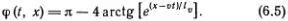
Эта функция представлена на рис. 6.3, б . На рис. 6.3, α изображена кривая зависимости φ от х в момент t = 0. Вдали от центра дислокации, расположенного в точке х = 0, атомы расположены вблизи положений равновесия, т. е. φ  π или φ
π или φ  -π. Атомы находятся далеко от положений равновесия лишь на расстояниях
-π. Атомы находятся далеко от положений равновесия лишь на расстояниях 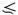 l v от центра. Мы можем поэтому называть l vполушириной дислокации или просто ее размером:
l v от центра. Мы можем поэтому называть l vполушириной дислокации или просто ее размером:
Если скорость дислокации равна нулю, то ее размер l v = l 0 зависит лишь от характеристик решетки. Размер равномерно движущейся дислокации t v с увеличением скорости уменьшается, причем это уменьшение определяется формулой
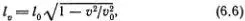
напоминающей преобразование длины при переходе в движущуюся систему координат в специальной теории относительности, только вместо скорости света с
Читать дальше


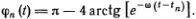

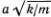 , представим mv 0 2как kα 2. Эта величина пропорциональна энергии, необходимой для растяжения пружины на величину порядка α . В знаменателе стоит произведение силы f 0на расстояние α , что, очевидно, пропорционально работе, которую надо затратить на преодоление барьера, отделяющего одну ямку от другой. Таким образом, l 0увеличивается при увеличении жесткости пружин и уменьшении силы со стороны «подкладки», привязывающей атомы к определенным местам. В дальнейшем будем считать, что упругая энергия kα 2значительно превосходит f 0 α , и, таким образом, величина l 0
, представим mv 0 2как kα 2. Эта величина пропорциональна энергии, необходимой для растяжения пружины на величину порядка α . В знаменателе стоит произведение силы f 0на расстояние α , что, очевидно, пропорционально работе, которую надо затратить на преодоление барьера, отделяющего одну ямку от другой. Таким образом, l 0увеличивается при увеличении жесткости пружин и уменьшении силы со стороны «подкладки», привязывающей атомы к определенным местам. В дальнейшем будем считать, что упругая энергия kα 2значительно превосходит f 0 α , и, таким образом, величина l 0 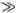 α .
α .
 π или φ
π или φ 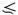 l v от центра. Мы можем поэтому называть l vполушириной дислокации или просто ее размером:
l v от центра. Мы можем поэтому называть l vполушириной дислокации или просто ее размером: