Александр Филиппов - Многоликий солитон

*) Это то же самое, что движение по сепаратрисе (см. (4.9)).

Наглядный образ волн на поверхности воды всем хорошо известен, однако эти волны представляют собой очень сложное явление, и для первого знакомства лучше найти хорошую «карикатуру». Именно так поступил Ньютон, предложивший простую модель распространения звуковой волны. Основная идея Ньютона сводилась к тому, что при распространении волны каждая частица среды колеблется подобно маятнику и движение каждой частицы влияет на движение всех окружающих ее частиц (ближайших соседей).

Дальнейшее упрощение состоит в том, что частицы, которые могут двигаться и одновременно деформироваться, Ньютон заменяет массивными грузиками, соединенными упругими пружинками, лишенными массы. Тогда кинетическая энергия частицы среды сосредоточена на грузиках, а потенциальная энергия упругой деформации частицы запасается в пружинах. (Рассуждения Ньютона здесь, конечно, модернизированы, но ход его мыслей передается достаточно точно.) Даже после этих серьезных упрощений модель реальной трехмерной среды еще слишком сложна. Следующий шаг приводит к задаче, которая решается точно.

Рассмотрим цепочку одинаковых частиц с массой m, соединенных упругими пружинками и движущихся по прямой. Физики называют эту систему моделью одномерного кристалла . Условимся поэтому называть частицы «атомами». Кавычки напоминают о том, что эти «атомы» пока не имеют никакого отношения к реальным физическим атомам. В дальнейшем мы их опускаем.

Пусть длина каждой пружинки в недеформированном состоянии равна α . Тогда покоящиеся атомы, перенумерованные, как указано на рис. 5.1, будут располагаться в точках с координатами nα , т. е. равновесное положение n -гo атома определяется координатой x 0 n= nα . Допустим теперь, что атомы отклонены от равновесного положения, так что координата n -гo атома равна х n (верхнее положение). Обозначим отклонение атома от равновесного положения буквой y n = х n- х 0 n= х n- nα и отложим отрезки y n над соответствующими точками x 0 n= nα .

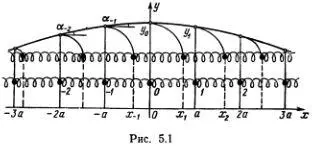
Соединив их плавной кривой, получим график, изображающий отклонения атомов от положений равновесия.

Плавная кривая получится, конечно, не всегда. Если отклонения каких-нибудь соседних атомов отличаются достаточно сильно, то у кривой будут резкие изломы. Мы поэтому предположим, что наклон графика отклонений очень медленно меняется, Т. е. разность двух последовательных углов α n по модулю много меньше самих углов.

При этом получится плавная кривая, мало изменяющаяся на расстоянии α , и наша модель будет достаточно точно воспроизводить смещения частицы в непрерывной (сплошной) среде. Другими словами, если мы хотим на модели воспроизвести распространение волны в сплошной среде (упругая волна в стержне, звуковая волна в органной трубе, волна на скрипичной струне и т. д.), нужно брать частички малыми и располагать их на малых расстояниях друг от друга. Сверх этого, длина волны λ должна быть много больше расстояния между атомами.

Картину распространения волн в такой цепочке можно изучить на очень простом устройстве, для изготовления которого нужна хорошая и достаточно длинная плоская резиновая лента и большие скрепки (см. рис. 5.2). Разумеется, эта система гораздо сложнее, чем идеальная одномерная цепочка, и к тому же очень несовершенна.

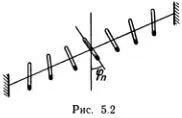
Главный ее недостаток — большие потери на трение в резине. Достоинство ее — небольшая скорость распространения волн. Это позволяет наблюдать бегущие по цепочке волны невооруженным глазом. Скорость распространения возбуждений можно изменять, утяжеляя скрепки. Интуитивно ясно, что с увеличением массы скрепок эта скорость должна уменьшаться.

Если скрепки закреплены на ленте в их центрах тяжести, так что сила тяжести не создает дополнительного вращательного момента, действующего на скрепки, то эта система вполне аналогична линейной цепочке. При этом угол φ n аналогичен отклонению y n , а роль массы грузика играет момент инерции скрепки.