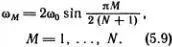Упражнение : рассмотрите простой случай, когда А 1= А 2= 1, t 1= t 2= 0, и покажите, что из-за несоизмеримости частот ω 1 и ω 2не существует такого значения Т , при котором y 1( Т ) = y 1(0), y 2( Т ) = y 2(0). Это и означает, что такое движение не может быть периодическим.
Ясно, что формулы (5.6) дают самое общее движение. Начальное состояние определяется координатами и скоростями частиц, т. е. значениями y 1(0), y 2(0), 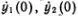 . Формулы (5.6) и их производные по времени позволяют найти неизвестные константы А 1, А 2, t 1, t 2через начальные координаты и скорости.
. Формулы (5.6) и их производные по времени позволяют найти неизвестные константы А 1, А 2, t 1, t 2через начальные координаты и скорости.
Замечательно, что нам удалось не только найти самое общее движение, но и разложить его на сумму самых простых из известных нам движений.
Конечно, в такой простой задаче то же самое можно было бы сделать и более простым способом. Например, если сложить и вычесть уравнения (5.1), то легко получить два независимых уравнения для ( y 1 + y 2) и ( y 1 - y 2), которые сразу решаются и приводят к формулам (5.6).
Однако наш чуть более длинный способ решения имеет преимущество — он легко обобщается на случай цепочки с любым числом частиц.
В качестве упражнения найдите частоты трех мод колебаний цепочки, состоящей из трех частиц. Для частот должен получиться результат: 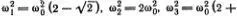
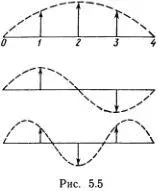
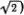 . Сами моды выглядят, как показано на рис. 5.5. Точный смысл этого рисунка (как и рис. 5.4) состоит в том, что моду с номером М можно представить в виде
. Сами моды выглядят, как показано на рис. 5.5. Точный смысл этого рисунка (как и рис. 5.4) состоит в том, что моду с номером М можно представить в виде
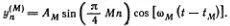
При заданном М = 1, 2, 3 индекс n пробегает три значения: n = 1, 2, 3, т. е. 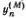 задает отклонение n-гo грузика в М -й моде. В случае двух частиц отклонения для двух мод можно написать в аналогичном виде
задает отклонение n-гo грузика в М -й моде. В случае двух частиц отклонения для двух мод можно написать в аналогичном виде
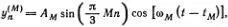
где М = 1, 2 и n = 1, 2.
Общую закономерность теперь нетрудно уловить и она наглядно ясна — нарисованные штрихами синусоиды соответствуют стоячим волнам. Легко также догадаться, что в цепочке из N частиц моду с номером М надо искать в виде
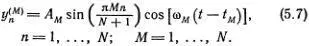
Уравнение движения для n -гo атома составляется точно так же, как уравнения (5.1), т. е.
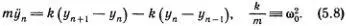
Это уравнение годится и для крайних атомов — первого и N -гo. Нужно только вспомнить, что крайние пружинки закреплены, т. е. у 0= y N +1= 0. Эти условия для предполагаемых решений (5.7) уже выполнены. Теперь должно быть ясно, как довести решение до конца. Надо подставить выражение (5.7) в уравнение (5.8) и заменить 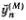 на -ω 2 My n (М). После несложных преобразований тригонометрических функций получится соотношение для ω 2 M , при выполнении которого все уравнения (5.8) удовлетворяются; это выражение мы приведем без вывода
на -ω 2 My n (М). После несложных преобразований тригонометрических функций получится соотношение для ω 2 M , при выполнении которого все уравнения (5.8) удовлетворяются; это выражение мы приведем без вывода
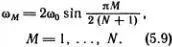
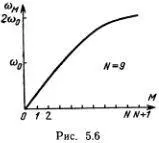
Эта зависимость частоты от номера моды изображена на рис. 5.6. Для мод с малыми номерами (низкочастотных и длинноволновых) частота пропорциональна номеру моды. Для высокочастотных мод (коротковолновых) частота выходит на предельное значение 2ω 0.
Формула (5.9) определяет спектр частот собственных колебаний (мод) цепочки. Не удивительно, что в цепочке из N частиц имеется ровно N собственных частот. Нетрудно понять и происхождение предельной частоты. Если один из грузиков колеблется слишком быстро, то соседние не успевают реагировать на его движение, и возбуждение не сможет распространяться вдоль цепочки. Этот вывод легко проверить, проделав простые опыты.
Читать дальше

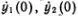 . Формулы (5.6) и их производные по времени позволяют найти неизвестные константы А 1, А 2, t 1, t 2через начальные координаты и скорости.
. Формулы (5.6) и их производные по времени позволяют найти неизвестные константы А 1, А 2, t 1, t 2через начальные координаты и скорости.
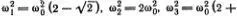
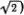 . Сами моды выглядят, как показано на рис. 5.5. Точный смысл этого рисунка (как и рис. 5.4) состоит в том, что моду с номером М можно представить в виде
. Сами моды выглядят, как показано на рис. 5.5. Точный смысл этого рисунка (как и рис. 5.4) состоит в том, что моду с номером М можно представить в виде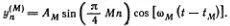
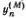 задает отклонение n-гo грузика в М -й моде. В случае двух частиц отклонения для двух мод можно написать в аналогичном виде
задает отклонение n-гo грузика в М -й моде. В случае двух частиц отклонения для двух мод можно написать в аналогичном виде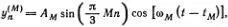
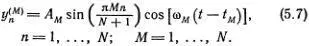
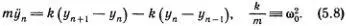
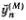 на -ω 2 My n (М). После несложных преобразований тригонометрических функций получится соотношение для ω 2 M , при выполнении которого все уравнения (5.8) удовлетворяются; это выражение мы приведем без вывода
на -ω 2 My n (М). После несложных преобразований тригонометрических функций получится соотношение для ω 2 M , при выполнении которого все уравнения (5.8) удовлетворяются; это выражение мы приведем без вывода