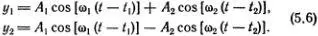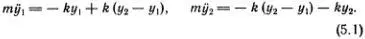
Действительно, сила, с которой левая пружина тянет первый грузик, равна произведению модуля упругости k на удлинение пружины y 1, и при y 1 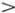 0 эта сила направлена в отрицательном направлении оси х . Так получается член ky 1*). Удлинение правой пружины равно ( y 2- y 1), и она тянет грузик с силой k( y 2- y 1). Это дает второй член в правой части первого уравнения. Точно так же находим силу, действующую на второй грузик.
0 эта сила направлена в отрицательном направлении оси х . Так получается член ky 1*). Удлинение правой пружины равно ( y 2- y 1), и она тянет грузик с силой k( y 2- y 1). Это дает второй член в правой части первого уравнения. Точно так же находим силу, действующую на второй грузик.
*) Предполагается, что упругие свойства пружины соответствуют закону Гука. Нелинейность зависимости силы отклонения вводится с помощью других, дополнительных источников силы.
На первый взгляд может показаться, что решить эти уравнения очень сложно. Однако они линейны, а это значит, что достаточно найти лишь некоторый запас решений. Их линейные комбинации, возможно, и дадут самое общее решение.
Для начала попробуем получить хоть какие-нибудь решения. В этом нам поможет физическая интуиция. Действительно, вслед за Ньютоном мы представляем себе простейшую бегущую волну как процесс распространения гармонического колебания от одной частицы к другой. Тогда стоячая волна — это просто установившиеся колебания всех частичек с разными амплитудами. Сделаем простейшее предположение: допустим, что все частицы колеблются гармонически и притом с одинаковой частотой ω, и посмотрим, что отсюда следует.
Для гармонических колебаний ускорение пропорционально отклонению, т. е. 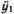 = -ω 2 y 1 и
= -ω 2 y 1 и 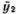 = -ω 2 y 2 . Подставляя это в уравнения (5.1), получаем простую линейную систему уравнений для y 1 и y 2:
= -ω 2 y 2 . Подставляя это в уравнения (5.1), получаем простую линейную систему уравнений для y 1 и y 2:
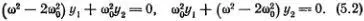
Здесь ω 0 2= k/m , а ω — не определенная пока частота наших гипотетических колебаний.
Ясно, что у этой системы уравнений относительно неизвестных y 1и y 2 есть неинтересное решение y 1 = y 2= 0. Пусть y 1 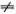 0. Тогда, выражения y 2через y 1из первого уравнения и подставляя полученное выражение во второе уравнение, найдем, что должно выполняться условие
0. Тогда, выражения y 2через y 1из первого уравнения и подставляя полученное выражение во второе уравнение, найдем, что должно выполняться условие
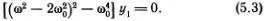
Так как y 1 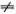 0, то выражение в квадратных скобках должно быть равно нулю *). Решая квадратное уравнение для ω 2, определяем два возможных значения частоты
0, то выражение в квадратных скобках должно быть равно нулю *). Решая квадратное уравнение для ω 2, определяем два возможных значения частоты
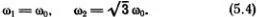
*) Если хотя бы в один момент времени y 1 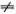 0, то множитель в квадратных скобках, не зависящий от времени, должен обращаться в нуль.
0, то множитель в квадратных скобках, не зависящий от времени, должен обращаться в нуль.
Если ω = ω 1, то из уравнений (5.2) следует, что y 2= y 1. Если ω = ω 2, то y 2= - y 1. Вспомним теперь, что y 1и y 2подчиняются уравнениям 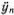 = -ω 2 y n , которые определяют их гармоническую зависимость от времени. При ω = ω 1= ω 0можно поэтому записать решение в виде
= -ω 2 y n , которые определяют их гармоническую зависимость от времени. При ω = ω 1= ω 0можно поэтому записать решение в виде
y 1= y 2= А 1cos [ω 1( t - t 1)], (5.5а)
а при ω = ω 2= 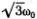 — в виде
— в виде
y 1= - y 2= А 2cos [ω 2( t - t 2)]. (5.5б)
Здесь A 1и А 2— произвольные амплитуды, а t 1и t 2— произвольные значения времени, определяющие фазу колебаний.
Эти два решения и дают две возможные моды колебаний нашей простейшей системы (рис. 5.4).
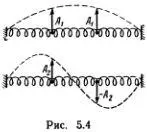
Они соответствуют двум нашим модам колебаний резинки, изображенным на рисунке штриховыми линиями. Конечно, это соответствие несколько условно, но, согласитесь, от карикатуры, сделанной двумя точками, нельзя требовать большего! Теперь можно снова воспользоваться линейностью уравнений (5.1) и написать решение в виде суммы решений (5.5а) и (5.5б):
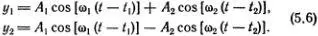
Это движение уже не сводится к простому гармоническому колебанию каждой из частиц. В общем случае, т. е. при произвольных значениях А 1, А 2, t 1, t 2, движение системы не будет даже периодическим.
Читать дальше

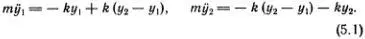
 0 эта сила направлена в отрицательном направлении оси х . Так получается член ky 1*). Удлинение правой пружины равно ( y 2- y 1), и она тянет грузик с силой k( y 2- y 1). Это дает второй член в правой части первого уравнения. Точно так же находим силу, действующую на второй грузик.
0 эта сила направлена в отрицательном направлении оси х . Так получается член ky 1*). Удлинение правой пружины равно ( y 2- y 1), и она тянет грузик с силой k( y 2- y 1). Это дает второй член в правой части первого уравнения. Точно так же находим силу, действующую на второй грузик.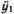 = -ω 2 y 1 и
= -ω 2 y 1 и 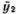 = -ω 2 y 2 . Подставляя это в уравнения (5.1), получаем простую линейную систему уравнений для y 1 и y 2:
= -ω 2 y 2 . Подставляя это в уравнения (5.1), получаем простую линейную систему уравнений для y 1 и y 2: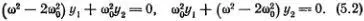
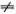 0. Тогда, выражения y 2через y 1из первого уравнения и подставляя полученное выражение во второе уравнение, найдем, что должно выполняться условие
0. Тогда, выражения y 2через y 1из первого уравнения и подставляя полученное выражение во второе уравнение, найдем, что должно выполняться условие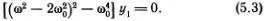
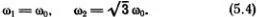
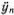 = -ω 2 y n , которые определяют их гармоническую зависимость от времени. При ω = ω 1= ω 0можно поэтому записать решение в виде
= -ω 2 y n , которые определяют их гармоническую зависимость от времени. При ω = ω 1= ω 0можно поэтому записать решение в виде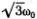 — в виде
— в виде