Вместо возвращающей упругой силы нужно рассматривать момент упругой силы, возникающий при скручивании резинки. Короче, аналогия здесь такая же, как аналогия колебаний грузика на пружинке и крутильных колебаний.
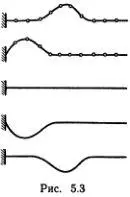
Еще одно существенное отличие нашей грубой модели от идеальной бесконечной цепочки связано с отражением волн от границ. Это происходит примерно так, как указано на рис. 5.3, где изображены графики отклонений грузиков или скрепок в последовательные моменты времени. Горбику соответствует смещение грузиков в положительном направлении оси х , впадине — в отрицательном. Когда горбик подходит к стенке, крайняя, закрепленная пружина начинает тянуть крайний грузик влево, он тянет соседние грузики, и в результате направо побежит впадина.
Если вместо продольных движений грузиков изучать их поперечные движения (в направлении оси у в плоскости ху ), то графики рис. 5.3 изображают форму поперечного импульса в цепочке. Наблюдать такие импульсы и волны можно с помощью мягкой и достаточно длинной резиновой трубки. Проделать соответствующие простые опыты несложно, и читатель может проявить здесь фантазию и изобретательность.
В резиновой трубке или ленте, закрепленных на концах, легко возбуждать стоячие волны . Особенно легко возбуждается колебание, в котором нетрудно узнать «полусинусоиду». При этом все точки колеблются в одинаковой фазе, и амплитуда колебаний максимальна в середине («пучность» стоячей волны). Длина такой стоячей волны равна удвоенной длине ленты *). Труднее возбудить колебание, в котором остается в покое середина («узел» стоячей волны). На всей ленте при этом укладывается «период синусоиды», и длина волны равна длине ленты. Чтобы возбудить такое колебание, нужно оттянуть ленты в противоположные стороны на равных расстояниях от краев, удерживая середину в покое. Легче наблюдать такую волну на приборчике со скрепками. Возбудив какие-либо колебания в этой цепочке (лучше всего это делать быстрым, легким щелчком по скрепке), можно просто остановить среднюю скрепку. При этом «выживет» колебание, в котором средняя скрепка покоится.
*) Ниже мы увидим, что синусоидальную стоячую волну можно представить в виде суммы двух одинаковых волн, бегущих в противоположных направлениях. Длина стоячей волны, по определению, совпадает с длиной этих бегущих волн.
Стоячие волны разных типов, в которых на всей длине ленты укладывается разное число N полуволн, называются нормальными модами колебаний (или просто модами ; это слово происходит от латинского modus, т. е. образ, способ). Моды с малыми значениями N называются низшими , а с большими — высшими . Моду с N = 1 естественно называть основной, она возбуждается легче всего. При произвольном начальном возбуждении нашей системы возбуждаются разные моды, однако высшие моды не только труднее возбуждаются, но и быстрее затухают из-за трения. Потому-то их и труднее наблюдать.
Понять, что такое моды и как они себя ведут, проще всего на модели одномерной цепочки конечной длины с закрепленными концами. Сначала посмотрим, как колеблется простейшая цепочка из двух атомов. Пусть их равновесные положения равны x 0 1= α и x 0 2= 2α, а крайние пружинки закреплены в точках x 0 0= 0 и x 0 3= 3α (см. рис. 5.1). Легко составить уравнения движения атомов.
Прежде чем это сделать, введем одно небольшое новшество в обозначениях. До сих пор нам приходилось иметь дело лишь с производными по времени, и мы их обозначали штрихом. При изучении колебаний в распределенных системах встречаются не только производные по времени, с помощью которых записываются скорости и ускорения отдельных частичек, но и производные по координате. Они характеризуют изменение отклонения при переходе от одной частицы к другой в один и тот же момент времени. Поэтому условимся обозначать производную по времени не штрихом, а точкой, а штрих сохраним для производной по координате. Теперь мы будем обозначать скорость n -гo грузика как 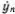 , а его ускорение — как
, а его ускорение — как 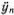 .
.
Уравнения движения грузиков можно тогда написать в виде
Читать дальше


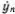 , а его ускорение — как
, а его ускорение — как 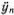 .
.










