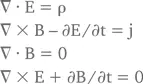Митио Каку - Гиперпространство - Научная одиссея через параллельные миры, дыры во времени и десятое измерение

Там же. Согласно Хендерсон, «четвертое измерение привлекало внимание таких видных представителей мира литературы, как Герберт Уэллс, Оскар Уайльд, Джозеф Конрад, Форд Мэдокс Форд, Марсель Пруст и Гертруда Стайн. Из музыкантов четвертым измерением живо интересовались Александр Скрябин, Эдгар Варез, Джордж Антейл, оно вдохновляло их поиски новых форм во имя высшей реальности» (там же, с. xix – xx).

Работа Ленина «Материализм и эмпириокритицизм» сегодня имеет большое значение по той причине, что она оставила заметный след в современной советской и восточноевропейской науке. К примеру, известное высказывание Ленина о «неисчерпаемости электрона» отражало диалектическую идею, согласно которой мы найдем новые уровни и противоречия при любой попытке проникнуть в суть материи. Так, галактики состоят из меньших по размеру звездных систем, которые в свою очередь содержат планеты, состоящие из молекул, которые состоят из атомов, содержащих электроны, а те, в свою очередь, «неисчерпаемы». Это один из вариантов теории «миров, заключенных в других мирах».

Владимир Ленин. Материализм и эмпириокритицизм // Карл Маркс, Фридрих Энгельс и Владимир Ленин. О диалектическом материализме. – М.: Прогресс, 1977. – С. 305–306.

Владимир Ленин. Материализм и эмпириокритицизм // Карл Маркс, Фридрих Энгельс и Владимир Ленин. О диалектическом материализме. – М.: Прогресс, 1977. – С. 305–306.

Процитировано в: Рукер «Четвертое измерение», с. 64.

Представим себе, что некий флатландец построил конструкцию из шести смежных квадратов, образующих подобие креста. С точки зрения флатландца, квадраты жестко соединены между собой. Из нельзя повернуть или иначе переместить относительно соединенных сторон. А теперь представим, что мы взяли эту конструкцию и решили отогнуть некоторые квадраты, чтобы образовался куб. Стыки между квадратами, жесткие в двумерном пространстве, в мире трех измерений легко поддаются, превращаясь в сгибы. Сложить куб настолько просто, что флатландец даже не заметит этого.

Но если флатландец очутится внутри куба, он обратит внимание на неожиданное явление. Каждый квадрат ведет в другой квадрат. «Внешней стороны» у куба нет. Всякий раз, когда флатландец переходит из одного квадрата в другой, он плавно, даже не замечая этого, сгибается под углом 90º в третьем измерении и попадает в следующий квадрат. Снаружи этот дом выглядит как самый обычный квадрат, но тот, кто войдет в него, обнаружит беспорядочное нагромождение квадратов, каждый из которых немыслимым образом ведет в следующий. Вошедшему покажется невероятным то, что этот единственный квадрат способен вместить шесть других квадратов.

Якоб Броновски «Восхождение человека» (Jacob Bronowski, The Ascent of Man, Boston: Little, Brown. 1974), с. 247.

Процитировано в: Абрахам Пайс «Научная деятельность и жизнь Альберта Эйнштейна» (Abraham Pais, Subtle Is the Lord: The Science and the Life of Albert Einstein, Oxford: Oxford University Press, 1982), с. 131.

Уравнения Максвелла выглядят так (мы принимаем с = 1):

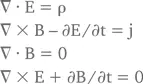
Вторая и последняя строчка – векторные уравнения, представляющие три уравнения каждое. Следовательно, всего уравнений Максвелла восемь.

Можно переписать их в релятивистской форме. Если ввести тензор Максвелла F μν= ∂ μ A ν – ∂ ν A μ, тогда уравнения сведутся к единственному:

Это и есть релятивистский вариант уравнений Максвелла.

Процитировано в: Абрахам Пайс «Научная деятельность и жизнь Альберта Эйнштейна», с. 239.

Процитировано в: Абрахам Пайс «Научная деятельность и жизнь Альберта Эйнштейна», с. 179.

Уравнения Эйнштейна выглядят так:

где T μν – тензор энергии-импульса, измеряющий содержание материи-энергии, а R μν – свернутый риманов тензор кривизны. Согласно этому уравнению, тензор энергии-импульса определяет степень кривизны, присутствующей в гиперпространстве.

Процитировано в: Абрахам Пайс «Научная деятельность и жизнь Альберта Эйнштейна», с. 212.