Стивен Вайнберг - Пояснюючи світ

Тепер розгляньмо зовнішні планети: Марс, Юпітер і Сатурн. У найпростішій версії теорії Коперника (або Тіхо Браге) кожна планета перебуває на постійній відстані не лише від Сонця, а й від якоїсь рухомої точки C ´ у просторі, яка перебуває на постійній відстані від Землі. Щоб знайти цю точку, накреслімо паралелограм (рис. 7б), першими трьома вершинами якого в порядку проти годинникової стрілки будуть С – положення Сонця, З – положення Землі, а також Р ´ – точка положення однієї з планет. Рухома точка C ´ є порожнім четвертим кутом цього паралелограма. Оскільки відрізок від З до С має фіксовану довжину, а відрізок від Р ´ до C ´ є протилежною стороною паралелограма, тобто також має фіксовану довжину, що дорівнює першому відрізку. Тому планета залишається на фіксованій відстані від C ´, що дорівнює відстані Землі від Сонця. Так само, оскільки відрізок від С до Р ´ має фіксовану довжину, то відрізок від З до C ´, що є протилежною стороною паралелограма, також має фіксовану довжину, що дорівнює першому відрізку. Тому точка C ´ залишається на фіксованій відстані від Землі, що дорівнює відстані планети від Сонця. Це особливий випадок теорії Птолемея, хоч той його ніколи не розглядав, у якому деферент є ніщо інше, як орбіта, якою рухається точка C ´ навколо Землі, а епіцикл є орбітою, якою Марс, Юпітер або Сатурн рухаються навколо C ´.

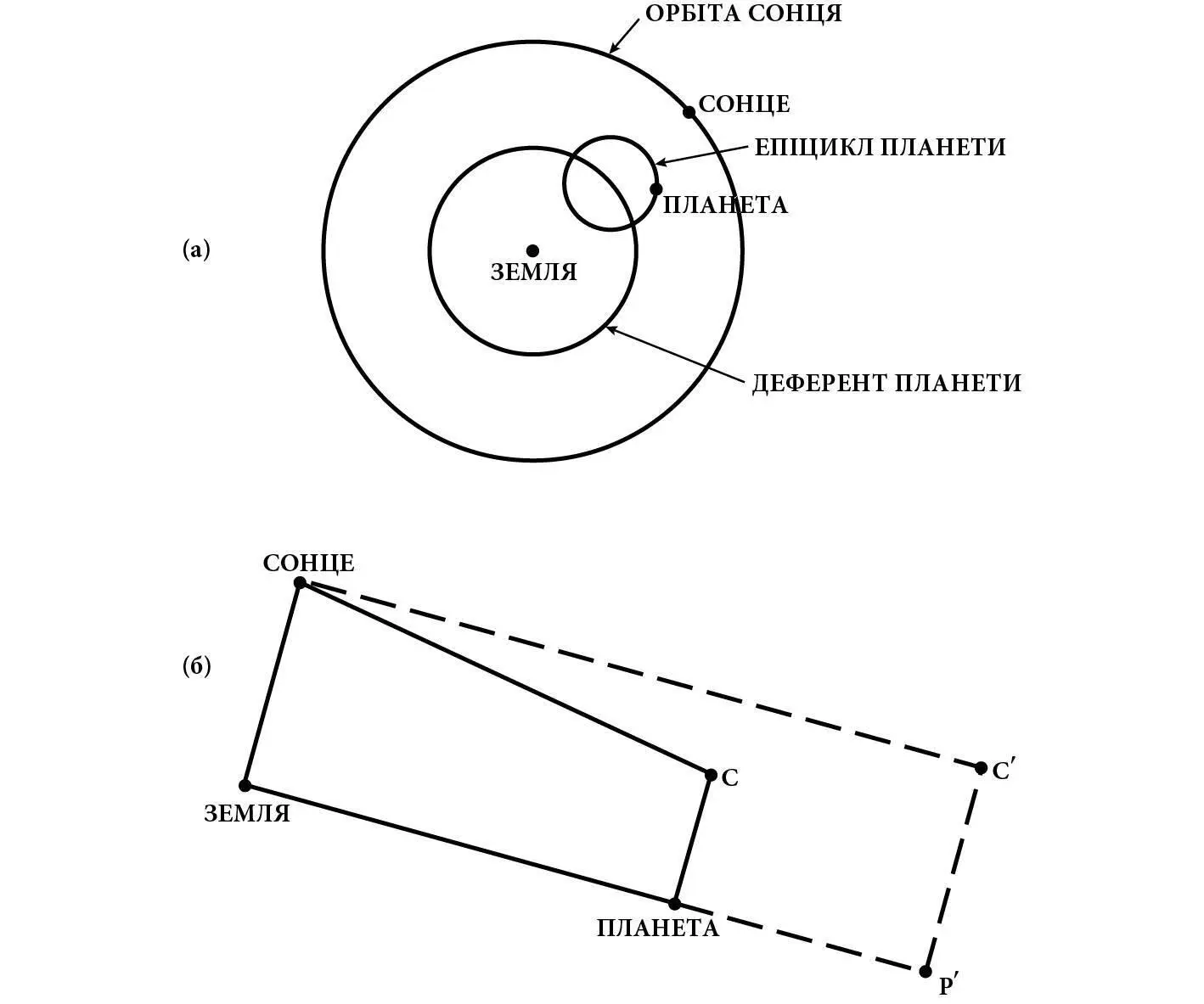
Рис. 7.Проста версія теорії епіциклу, яку описав Птолемей: a) гаданий рух однієї з внутрішніх планет – Меркурія або Венери; б) гаданий рух однієї із зовнішніх планет – Марса, Юпітера або Сатурна. Планета P обертається по епіциклу навколо точки C за один рік, при цьому відрізок від C до P завжди паралельний відрізку від Землі до Сонця, тоді як точка C обертається навколо Землі по деференту за довший час (пунктирні лінії позначають особливий випадок теорії Птолемея, у якому вона еквівалента теорії Коперника).

Знову ж таки, коли йдеться про видиме положення в небі Сонця та планет, можна помножити мінливу відстань будь-якої планети від Землі на якусь сталу, не змінюючи видимостей, якщо помножити радіуси епіциклу та деферента на якийсь постійний множник, вибраний окремо для кожної зовнішньої планети. Хоч ми вже не отримуємо паралелограма, відрізок між планетою та C залишається паралельним відрізку від Землі до Сонця. Видимий рух кожної зовнішньої планети в небі не зміниться від такого перетворення, якщо тільки не змінити співвідношення радіусів деферента й епіциклу кожної планети. Це проста версія теорії, яку запропонував Птолемей для зовнішніх планет. Згідно з цією теорією, планета робить один повний оберт навколо C по своєму епіциклу за 1 рік, тоді як C обертається по деференту за час, який ця планета реально витрачає на один повний оберт навколо Сонця: 1,9 року для Марса, 12 років для Юпітера та 29 років для Сатурна.

Зокрема, оскільки співвідношення радіусів деферента та епіциклу не змінюється, має бути збережена рівність:

r епі/ r деф = r з/ r п,

де r епі та r деф знову позначають радіуси епіциклу й деферента у схемі Птолемея, а r п та r з – радіуси орбіт планети й Землі в теорії Коперника (або те саме, що радіуси орбіт планет навколо Сонця та Сонця навколо Землі в теорії Тіхо Браге). Знову ж таки, усе сказане вище описує не те, як Птолемей дійшов своєї теорії, а лише те, чому ця теорія працювала так добре.

14. Місячний паралакс

Припустімо, що кут між напрямком до Місяця, який можна спостерігати з точки O на поверхні Землі, і напрямком до зеніту становить ζ´ (дзета штрих). Місяць рухається постійно й рівномірно навколо центра Землі, тому, використовуючи результати регулярних спостережень Місяця, можна обчислити напрямок від центра Землі C до Місяця M у той самий момент і, зокрема, обчислити кут ζ між напрямком від C до Місяця та напрямком до зеніту від центра Землі, що проходить через точку O . Кути ζ та ζ´ трохи відрізняються, бо радіус Землі r з не такий малий, як порівняти з відстанню до Місяця від центра Землі d , щоб ним можна було знехтувати. Саме з цієї різниці кутів Птолемей зумів обчислити співвідношення d/r з.

Точки C, O та M утворюють трикутник, у якому кут при вершині C дорівнює ζ, кут при вершині O дорівнює 180° − ζ´, а кут при вершині M дорівнює 180° − ζ − (180° − ζ´) = ζ´ − ζ, оскільки сума кутів будь-якого трикутника становить 180° (див. рис. 8). Ми можемо обчислити співвідношення d/r з зі значень цих кутів значно легше, ніж це робив Птолемей. Для цього ми використаємо теорему сучасної тригонометрії: у будь-якому трикутнику довжини сторін пропорційні синусам протилежних кутів (синуси розглядаємо в технічній примітці 15). Кут, протилежний відрізку СО довжиною r з, дорівнює ζ´ − ζ, а кут, протилежний відрізку CM довжиною d , дорівнює 180° − ζ´, тому: