хорда θ = 2sin(θ/2).
Отже, будь-яке обчислення, яке можна виконати за допомогою синусів, можна виконати і за допомогою хорд, хоча здебільшого воно менш зручне.
16. Горизонти
Зазвичай роздивитися навкруги на вулиці нам заважають навколишні дерева, будинки або якісь інші перепони. З вершини гори ясної днини можна побачити значно далі, але наше поле зору все ще обмежене горизонтом, за яким лінії прямої видимості закриває сама Земля. Давньоарабський астроном аль-Біруні описав розумний метод використання цього знайомого всім явища для вимірювання радіуса Землі, знаючи при цьому тільки одну відстань – висоту гори.
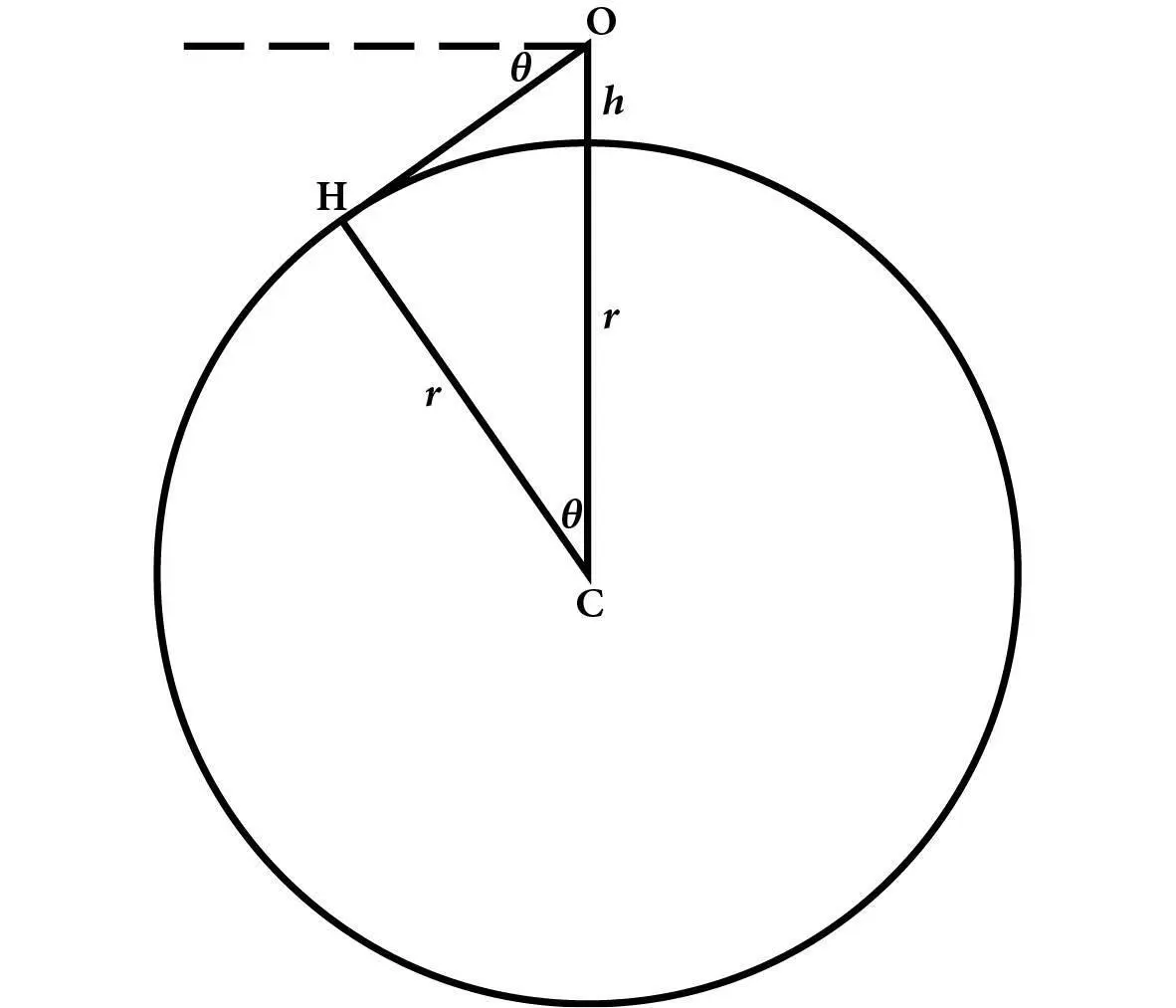
Рис. 10.Використання аль-Біруні горизонтів для вимірювання розміру Землі. O – спостерігач на горі заввишки h; H – горизонт, як його бачить цей спостерігач; відрізок від H до O – дотична до земної поверхні в точці H, а тому утворює прямий кут із відрізком від центра Землі C до H.
Уявімо, що спостерігач з точки O на вершині гори може бачити аж до якоїсь точки H на земній поверхні, у якій лінія прямої видимості дотична до цієї поверхні (див. рис. 10). Ця лінія прямої видимості перпендикулярна лінії, що з’єднує H із центром Землі C , тому трикутник OCH прямокутний. Лінія прямої видимості проходить нижче від горизонтального напрямку на певний кут θ, який є малим, бо Земля велика й горизонт значно віддалений. Кут між лінією прямої видимості та вертикальним напрямком униз від вершини гори дорівнює тоді 90° − θ. Тому, оскільки сума кутів будь-якого трикутника дорівнює 180°, гострий кут трикутника в центрі Землі дорівнює 180° − 90° − (90° − θ) = θ. Прилеглий до цього кута катет CH має довжину, що дорівнює радіусу Землі r , а довжина гіпотенузи CO цього трикутника дорівнює r + h , де h – висота гори. Згідно із загальним визначенням, косинус будь-якого кута дорівнює відношенню прилеглої сторони до гіпотенузи, що в цьому випадку дає:
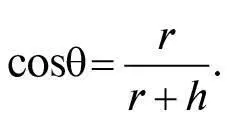
Щоб розв’язати це рівняння для r , зверніть увагу, що обернене рівняння таке: 1 + h/r = 1/cosθ, тому, віднявши 1 з обох частин рівняння, а потім взявши обернене значення знову, ми отримаємо:
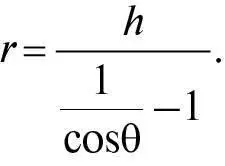
Наприклад, на одній горі в Індії аль-Біруні знайшов кут θ = 34´, для якого cosθ = 0,999951092, а 1/cosθ − 1 = 0,0000489. Отже,
r = h /0,0000489 = 20450 h.
Аль-Біруні повідомив, що висота тієї гори становила 652,055 ліктя (зі значно більшою точністю, ніж він міг би якось досягти), що тоді насправді дає r = 13,3 млн ліктів, при тому, що сам він наводить результат у 12,8 млн ліктів. Чому аль-Біруні помилився, мені не відомо.
17. Геометричне доведення теореми про середній градус швидкості
Припустімо, що ми будуємо графік зміни швидкості залежно від часу за рівномірного прискорення (швидкість – по вертикальній осі, а час – по горизонтальній). Цей графік буде представлений прямою лінією, що зростає від нульової швидкості в нульовий час до кінцевої швидкості в кінцевий час. У кожен дуже малий проміжок часу пройдена відстань є добутком швидкості в цей момент часу (якщо цей проміжок часу достатньо короткий, то швидкість змінюється на мізерно малу величину) на тривалість цього часового проміжку. Тобто пройдена відстань дорівнює площі вузького прямокутника, висотою якого є висота графіка в цей момент часу, а шириною – цей дуже малий часовий проміжок (див. рис. 11a). Ми можемо заповнити площу під графіком від початкового до кінцевого часу такими вузькими прямокутниками, і тоді загальна пройдена відстань дорівнюватиме загальній площі всіх цих прямокутників, тобто площі під графіком (див. рис. 11б.)
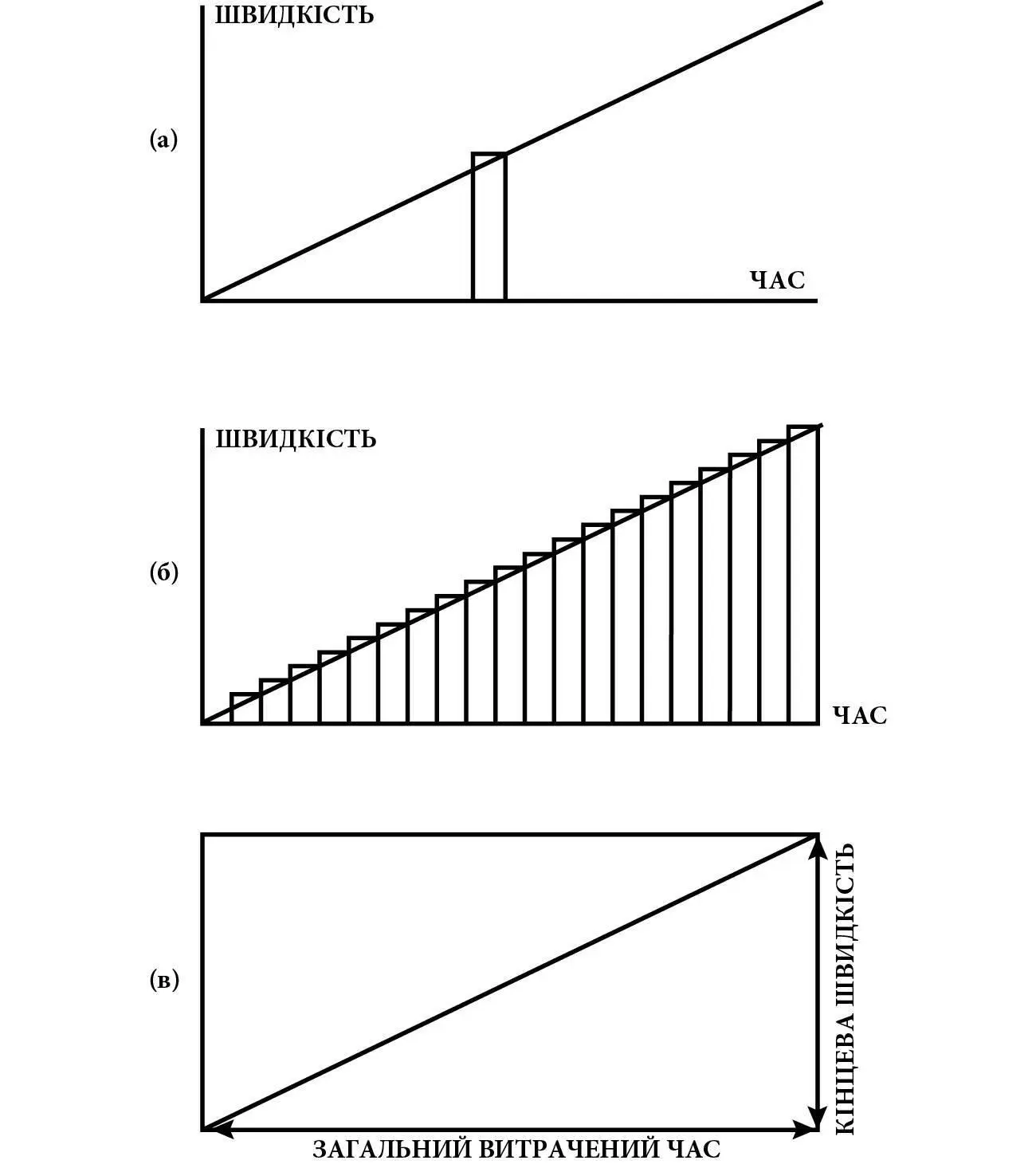
Рис. 11.Геометричне доведення теореми про середній градус швидкості. Похила лінія – це графік зміни швидкості залежно від часу для тіла, що рівномірно прискорюється зі стану спокою: a) ширина маленького прямокутника – це короткий часовий проміжок; його площа близька до відстані, пройденої тілом за цей проміжок; б) час упродовж періоду рівномірного прискорення, розбитий на короткі проміжки; у міру збільшення кількості прямокутників сума їхніх площ стає дедалі ближчою до площі під похилою лінією; в) площа під похилою лінією дорівнює половині добутку витраченого часу на кінцеву швидкість.
Читать дальше


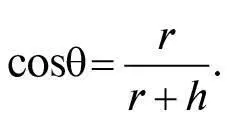
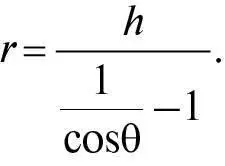






![Стивен Вайнберг - Первые три минуты [litres]](/books/398000/stiven-vajnberg-pervye-tri-minuty-litres-thumb.webp)




