Звісно, якими б вузькими ми не зробили прямокутники, лише наближено можна сказати, що площа під графіком дорівнює загальній площі цих прямокутників. Але ми можемо зробити ці прямокутники наскільки завгодно вузькими, а отже, зробити наближення наскільки завгодно хорошим. Уявивши нескінченну кількість нескінченно вузьких прямокутників, ми можемо дійти висновку, що пройдена тілом відстань дорівнює площі під графіком зміни швидкості залежно від часу.
Ці міркування не змінилися б і тоді, якби прискорення не було рівномірне і графік не був би прямою лінією. Фактично ми щойно вивели фундаментальний принцип інтегрального числення: якщо побудувати графік зміни в часі будь-якої величини, то зміна цієї величини за будь-який часовий проміжок дорівнює площі під кривою в межах цього проміжку. Але для рівномірної зміни величини, як за рівномірного прискорення, цю площу можна обчислити за простою геометричною теоремою.
Ця теорема говорить нам, що площа прямокутного трикутника дорівнює половині добутку довжин двох сторін, прилеглих до прямого кута, тобто сторін, що не є гіпотенузою. Це випливає одразу з того факту, що ми можемо звести два такі трикутники разом, щоб утворити прямокутник, площа якого є добутком довжин двох його сторін (див. рис. 11в). У нашому випадку двома сторонами, прилеглими до прямого кута, є кінцева швидкість та загальний витрачений час. Пройдена відстань є площею прямокутного трикутника з такими вимірами або половиною добутку кінцевої швидкості на загальний витрачений час. Але оскільки швидкість збільшується від нуля з постійним темпом, її середнє значення дорівнює половині її кінцевого значення, тому пройдена відстань дорівнює середній швидкості, помноженій на витрачений час. У цьому й полягає теорема про середній градус швидкості.
18. Еліпси
Еліпс – це певний різновид замкненої кривої на плоскій поверхні. Є як мінімум три різні способи чітко описати таку криву.
Визначення перше
Еліпс – це набір точок на площині, який задовольняє умови рівняння:
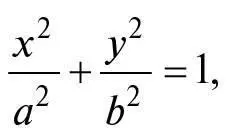 (1)
(1)
де x – відстань від центра еліпса будь-якої точки на еліпсі вздовж однієї осі, y – відстань від центра до тієї самої точки вздовж осі, перпендикулярної першій, а а і b – додатні числа, що характеризують розмір та форму еліпса, вибрані так, що а ≥ b . Для чіткості опису зручно уявляти собі вісь x горизонтальною, а вісь y вертикальною, хоча, звісно, вони можуть пролягати в будь-яких двох взаємно перпендикулярних напрямках. З рівняння (1) випливає, що відстань 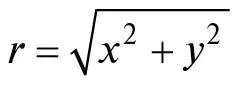 будь-якої точки на еліпсі від центра при x = 0, y = 0 задовольняє умови
будь-якої точки на еліпсі від центра при x = 0, y = 0 задовольняє умови
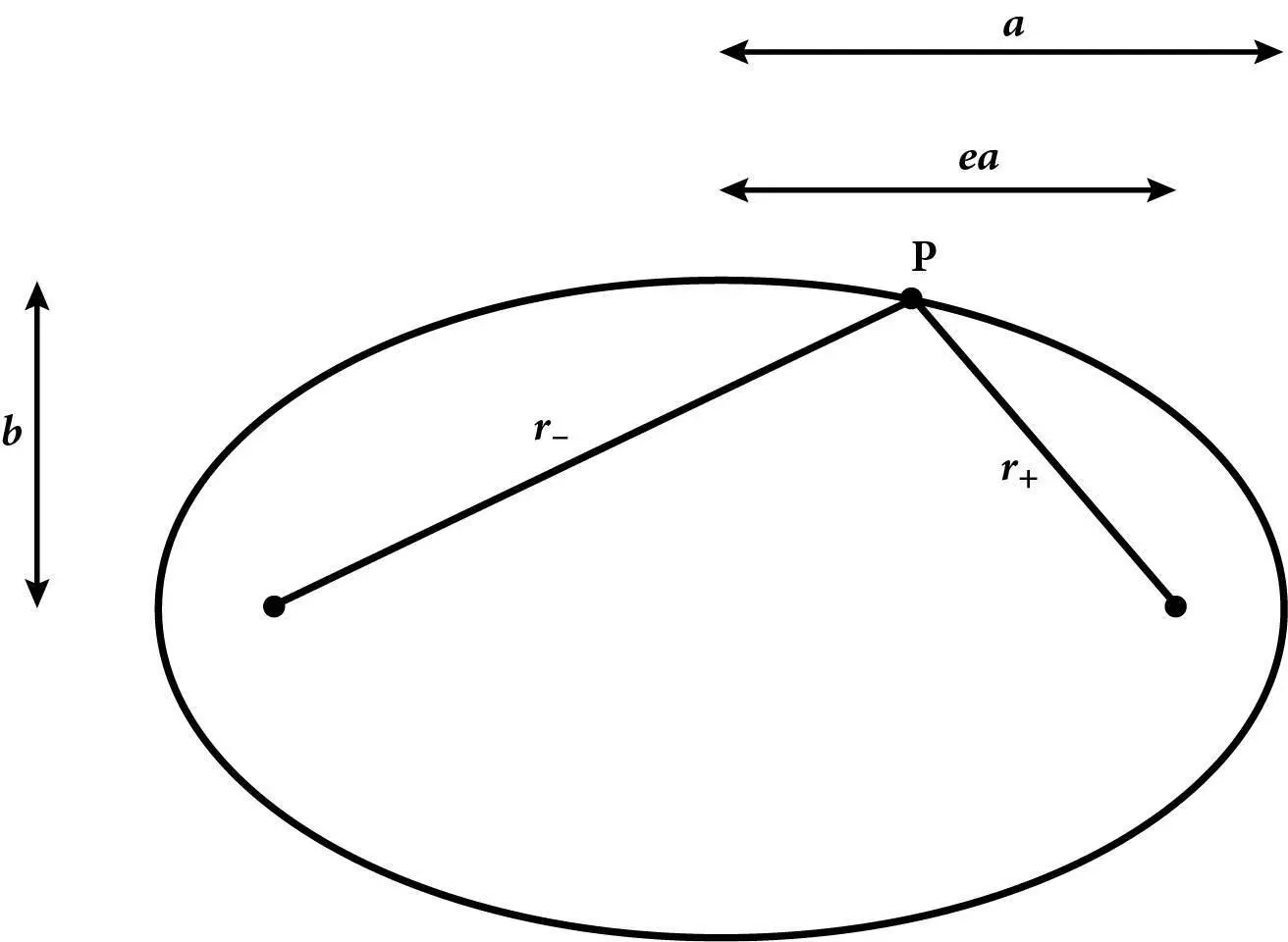
Рис. 12. Елементи еліпса.Позначені точки всередині еліпса – це два її фокуси; а і b – це велика та мала піввісі еліпса; а ea – відстань від кожного фокуса до центра еліпса. Сума довжин r+ та r– двох ліній від фокусів до точки P – дорівнює 2a незалежно від положення P на еліпсі. Зображений тут еліпс має еліптичність e = 0,8.
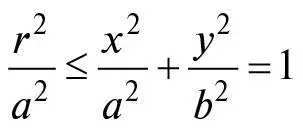 та
та 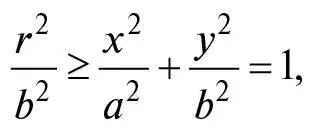
тому для будь-якої точки на еліпсі справедливо:
b ≤ r ≤ a (2)
Зверніть увагу, що там, де еліпс перетинає горизонтальну вісь, ми маємо y = 0, тому x 2 = a 2, а отже, x = ± a . Отже, рівняння (1) описує еліпс, довгий діаметр якого проходить від − a до + a в горизонтальному напрямку. Крім того, там, де еліпс перетинає вертикальну вісь, ми маємо x = 0, тому y 2 = b 2, а отже, y = ± b , а з цього випливає, що рівняння (1) описує еліпс, короткий діаметр якого проходить у вертикальному напрямку від − b до + b (див. рис. 12). Параметр а називають великою піввіссю еліпса. Ексцентриситет еліпса зручно визначити як
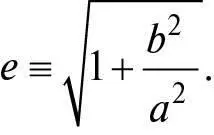 (3)
(3)
У загальному випадку ексцентриситет має значення між 0 та 1. Еліпс з e = 0 є колом з радіусом а = b . Еліпс з e = 1 такий сплющений, що є лише відрізком горизонтальної осі з y = 0.
Читать дальше

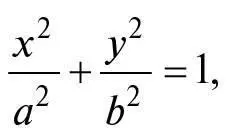 (1)
(1)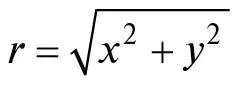 будь-якої точки на еліпсі від центра при x = 0, y = 0 задовольняє умови
будь-якої точки на еліпсі від центра при x = 0, y = 0 задовольняє умови
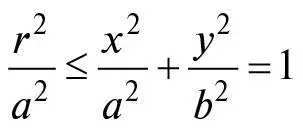 та
та 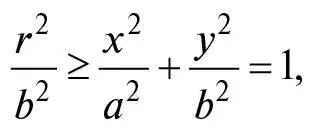
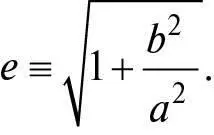 (3)
(3)




![Стивен Вайнберг - Первые три минуты [litres]](/books/398000/stiven-vajnberg-pervye-tri-minuty-litres-thumb.webp)




