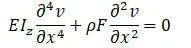
Уравнения, описывающие изгибно-крутильные колебания:
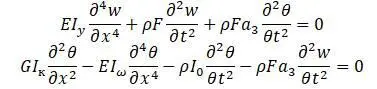
Граничные условия при x = 0 и x = l :
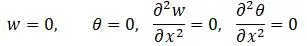
Граничные условия удовлетворяются при:
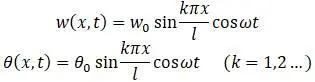
Собственные частоты определяются из формулы:
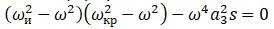
Частоты изгибных и крутильных колебаний 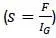 :
:
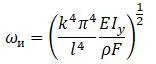
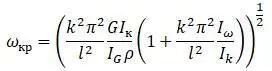
Собственные частоты колебаний:
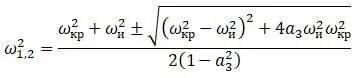
При a 3= 0 центр тяжести и центр изгиба совпадают,
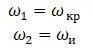
__
Как видно, формулы Тимошенко и по справочнику [32] для определения поперечных и изгибных колебаний почти полностью совпадают.
Однако, Тимошенко указывает о независимости от и необходимости применения метода Релея-Ритца.
__
Таким образом, для вала с мешалками как для балки по приведенной выше теории должны быть рассчитаны поперечные колебания, например, для неразрезной балки на трех опорах.
Затем должны быть рассчитаны крутильные колебания. Но в процессе перемешивания крутильных колебаний может и не возникать, в этом случае критические частоты будут строго соответсвовать поперечным частотам собственных колебаний. В случае наличия крутильных колебаний, их необходимо определить и проверку прочности выполнить для поперечных и крутильных колебаний.
Метод определения критической скорости по работе Тимошенко [31], где колебания связываются с эксцентриситетом необходимо считать некорректным. Колебания возникнут и при отсутсвиии эксцентриситета, однако, условия для статической балки и вращающегося вала с учетом эксцентриситета будут отличаться.
__
Тимошенко указывает о необходимости численного выполнения расчетов колебаний в работе [30]. То есть в том числе маститый специалист признает превосходство численных методов над ручными расчетами.
__
Итак, можно сделать следующий вывод: теорию колебаний можно применять для ручного расчета на практике, но она больше необходима для глубокого понимания физики процесса колебаний, а расчеты должны выполняться методом конечных элементов в специальном программном пакете, например, ANSYS.
Расчет валов методом конечных элементов
В динамической задаче воздействие внешних сил является функцией времени. Напряженно-деформированное состояние зависит от времени. Время является дополнительным параметром, усложняющим расчет по сравнению со статическими расчетами.
Уравнения движения динамической системы выводятся с применением принципа Даламбера, на основе принципа возможных перемещений, на основе вариационного принципа Гамильтона.
Метода Даламбера удобно применять для систем с небольшим числом степеней свободы [20,с.486], к которым относятся валы с мешалками. Но вариационный подход Гамильтона является обобщением методов. Поэтому расчет вала с мешалками методом конечных элементов приведем на основе вариационного подхода Гамильтона.
Принцип Гамильтона записывается в форме [20]:
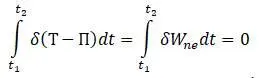
( Т и П – кинетическая и потенциальная энергии, W ne – силы демпфирования).
Функционал Лагранжа [20]:
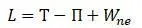
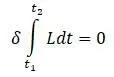
Функционал Лагранжа по принципу Гамильтона при возможных перемещениях удовлетворяет условиям совместности и граничным условиям на контуре в течении времени от t 1 до t 2 и имеет стационарное значение.
Читать дальше
Конец ознакомительного отрывка
Купить книгу
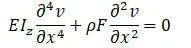
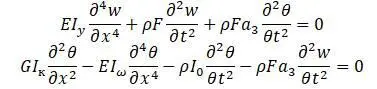
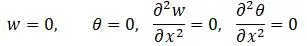
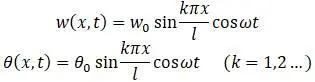
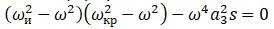
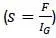 :
: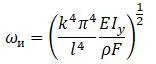
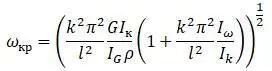
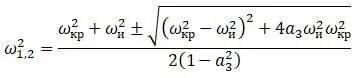
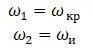
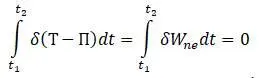
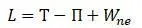
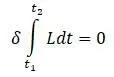
![Константин Ефанов - Теория расчета нефтяных аппаратов высокого давления [litres самиздат]](/books/437559/konstantin-efanov-teoriya-rascheta-neftyanyh-apparato-thumb.webp)










