Центробежная сила:
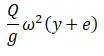
Упругая сила:
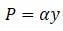
Приравнивая:
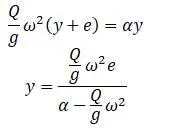
На невысокой угловой скорости с эксцентриситетом близким к нулю, прогиб незначителен. С увеличением ω прогиб увеличивается и при 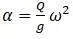 становится
становится 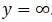 .
.
В этом случае угловая скорость является критической скоростью:
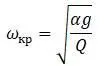
При превышении критической скорости формула равновесия:
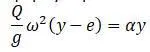
(изменился знак между y и e с «+» на «+»).
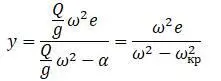
Формула показывает, что с увеличением частоты, прогиб уменьшается.
После этого Тимошенко [31,с.258] принимает для анализа вала модель, в которой сам вал вращается вокруг своей оси (изогнутой оси) с частотой ω, и плоскость вала вращается вокруг прямой оси с такой же частотой ω.
В этом случае на вал будет действовать сила
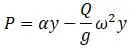
Работа центробежной силы:
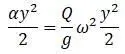
Из этой формулы получается такая же формула для критической частоты.
Оценивается влияние массы вала на значение критической частоты. Используется метод Релея. Задается вид кривой изгиба вала. Этим система вала преобразуется в систему с одной степенью свободы. Для вала с одной мешалкой ( η – прогиб):
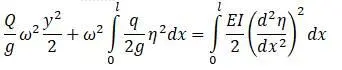
Для нескольких мешалок на валу:
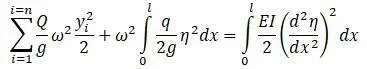
Второй член левой части формулы относится к работе центробежной силы.
Некорректность этих формул в том, что они не учитывают наклон плоскостей мешалок к оси вала.
Наклон мешалок за счет появления моментов сил инерции противодействует изгибу вала, т.е. повышает жесткость и увеличивает значение критической частоты.
Тимошенко [31,с.260] рассматривает вал с 4 дисками:
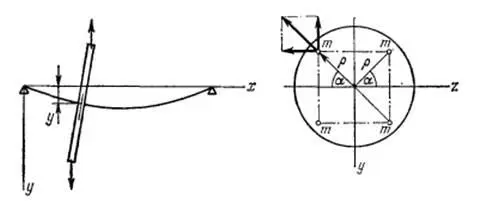
Горизонтальные силы уравновешиваются, вертикальные силы приводятся к паре сил и силе в плоскости xy . Пара сил:
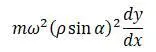
Все пары приводятся к паре 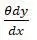 (θ – момент инерции мешалки относительно оси z).
(θ – момент инерции мешалки относительно оси z).
Пара производит работу против искривления оси вала 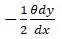
Формула для определения критической частоты:
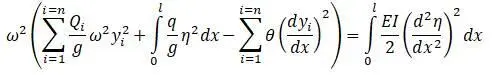
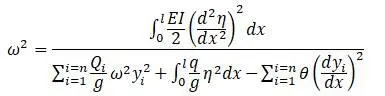
Тимошенко называет приведенную формулу общим решением о разыскании критической угловой скорости [31,с.260].
__
По изложенной выше теории поперечных колебаний можно определять собственные частоты колебаний валов для различных конструктивных компоновок перемешивающих устройств, а затем по приведенным выше формулам рассчитывать критические обороты вала.
Совместное действие поперечных и крутильных колебаний на вал
Тимошенко С.П. в работе [30,с.427] подробно рассмотрел проблему совместного действия изгибных и крутильных колебаний на балку. Для рассматриваемого им случая изгибные колебания проходили не в плоскости симметрии стержня, в результате чего возникают крутильные колебания. В нашем случае крутильные колебания возникают при вращении вала с мешалками. Однако, выводы полученные Тимошенко могут быть применены для анализа совместного действия поперечных и крутильных колебаний вала с мешалками.
Читать дальше
Конец ознакомительного отрывка
Купить книгу
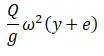
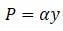
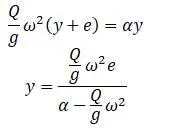
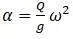 становится
становится 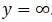 .
.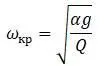
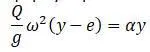
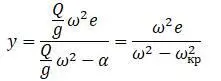
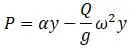
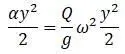
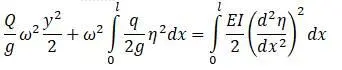
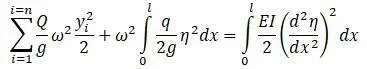

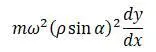
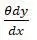 (θ – момент инерции мешалки относительно оси z).
(θ – момент инерции мешалки относительно оси z).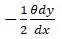
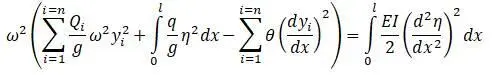
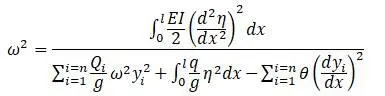
![Константин Ефанов - Теория расчета нефтяных аппаратов высокого давления [litres самиздат]](/books/437559/konstantin-efanov-teoriya-rascheta-neftyanyh-apparato-thumb.webp)










