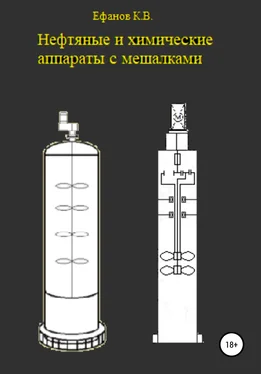
Для вертикальной нагрузки кривая прогиба:
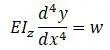
(w – интенсивность распределения поперечной нагрузки, за положительное направление принимается верх)
Нагрузку, распределенную вдоль центральной оси заменяют нагрузкой, проходящей через центр сдвига, и распределенный крутящий момент интенсивностью wc .
Крутящий момент:
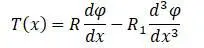
R – крутильная жесткость, R 1 – жесткость стесненного кручения.
Дифференцируя получается:
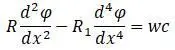
Уравнение показывает связь между изгибом и кручением при приложении статической нагрузки вдоль оси.
Интенсивность поперечных сил инерции 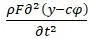
Интенсивность моментов инерции 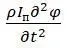
I п – центральный полярный момент инерции сечения вала.
Формулы для совместных изгибных и крутильных колебаний:
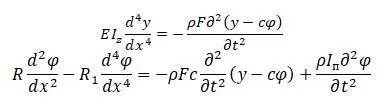
Вал колеблется в одной из собственных форм колебаний.
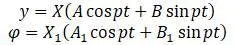
р – круговая частота колебаний,
Х , Х 1 – нормальные функции, решения которых отыскиваются для удовлетворения граничным условиям.
После подстановки:
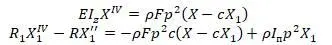
Тимошенко приводит пример стержня со свободно опертыми концами:
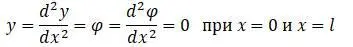
Функции Х и Х 1 в этом случае:
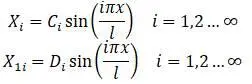
C i и D i – произвольные постоянные.
Вводятся обозначения:
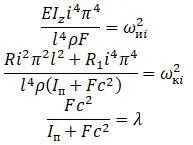
После подстановки получается:
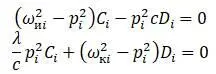
Решения для C i и D i находятся в случае, если определитель уравнений равен нулю.
В этом случае частотное уравнение:
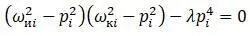
Из этой формулы:
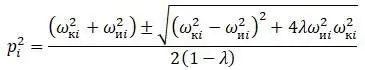
Для случая совпадения центра тяжести с центром сдвига, то есть с = 0 и λ =0 :
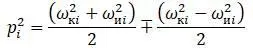
Из формулы получаются две системы значений частот:
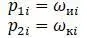
Полученные частоты являются несвязанных друг с другом и независимых друг от друга частот изгибных (поперечных) и крутильных колебаний. Аналогичные результаты получаются для стержней с другими условиями закрепления концов.
Связанные изгибно-крутильные колебания можно найти методом Релея-Ритца [30,с.430].
__
Итак, по представленным данным Тимошенко возможен раздельный расчет на поперечные и крутильные колебания , либо расчет на изгибно-крутильные колебания методом Релея-Ритца.
Результат этого вывода может быть использован конструкторами для упрощения проблем проектирования валов с мешалками. То есть выполнять расчет поперечных колебаний и расчет крутильных колебаний по отдельности. Для определенных технических целей необходимо выполнение только одного из видов расчетов. Изложенная теория даст более глубокое понимание физики колебаний вала. Однако, правильно выполнять расчет на изгибно-крутильные колебания вала с мешалками.
Расчет изгибно-крутильных колебаний вала с мешалками по данным [32].
Рассмотрим шарнирно опертый стержень [32,с.200]. Система уравнений распадется на две независимые системы. Уравнение, описывающее только изгибные колебания в плоскости симметрии:
Читать дальше
Конец ознакомительного отрывка
Купить книгу
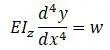
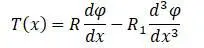
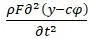
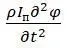
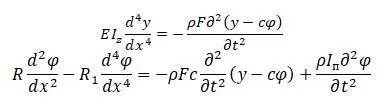
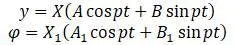
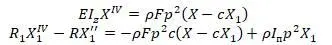
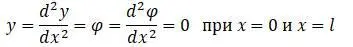
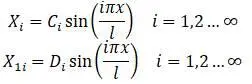
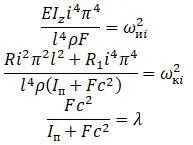
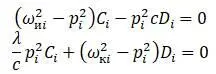
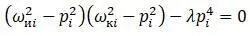
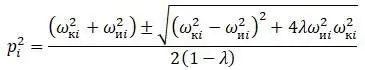
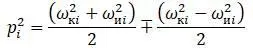
![Константин Ефанов - Теория расчета нефтяных аппаратов высокого давления [litres самиздат]](/books/437559/konstantin-efanov-teoriya-rascheta-neftyanyh-apparato-thumb.webp)










