Константин Ефанов - Аппараты с перемешивающими устройствами
Здесь есть возможность читать онлайн «Константин Ефанов - Аппараты с перемешивающими устройствами» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Год выпуска: 2021, ISBN: 2021, Издательство: Array SelfPub.ru, Жанр: Физика, Технические науки, на русском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Аппараты с перемешивающими устройствами
- Автор:
- Издательство:Array SelfPub.ru
- Жанр:
- Год:2021
- ISBN:978-5-532-03611-6
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Аппараты с перемешивающими устройствами: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Аппараты с перемешивающими устройствами»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
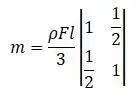
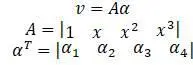
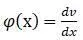
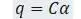
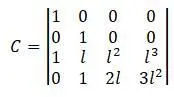
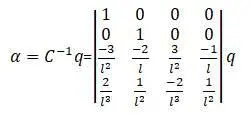
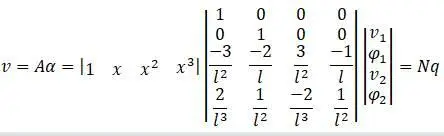
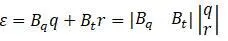
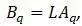
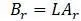
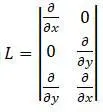
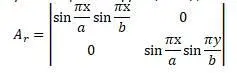
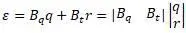 :
: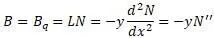
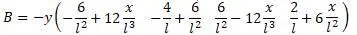
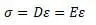
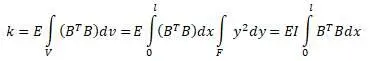
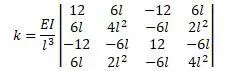
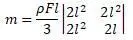
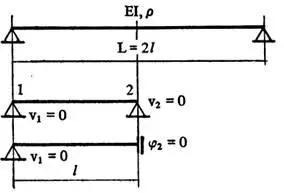
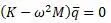 матрицы получится:
матрицы получится: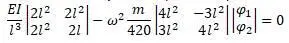
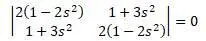
![Константин Ефанов - Теория расчета нефтяных аппаратов высокого давления [litres самиздат]](/books/437559/konstantin-efanov-teoriya-rascheta-neftyanyh-apparato-thumb.webp)










