§ 7. Вторые производные векторных полей
Пока мы имели дело только с первыми производными. А почему не со вторыми? Из вторых производных можно составить несколько комбинаций:
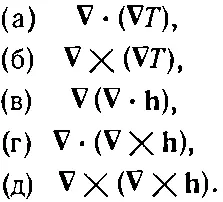 (2.45)
(2.45)
Вы можете убедиться, что никаких иных комбинаций быть не может.
Посмотрим сперва на вторую комбинацию (б). Она имеет ту же форму, что и
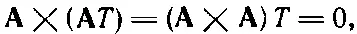
потому что А× Авсегда нуль. Значит,
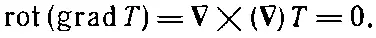 (2.46)
(2.46)
Можно понять, как это получается, если расписать одну из компонент:
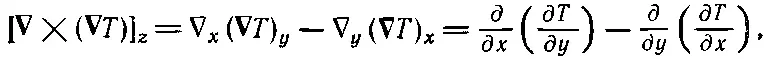 (2.47)
(2.47)
что равно нулю [по уравнению (2.8)]. Это же верно и для других компонент. Стало быть, ∇×( ∇T)=0 для любого распределения температур, да и для всякой скалярной функции.
Возьмем второй пример. Посмотрим, нельзя ли получить нуль другим путем. Скалярное произведение вектора на векторное произведение, содержащее этот вектор, равно нулю
 (2.48)
(2.48)
потому что А× Вперпендикулярно к Аи не имеет тем самым составляющих вдоль А. Сходная комбинация стоит в списке (2.45) под номером (г):
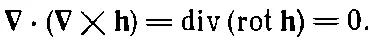 (2.49)
(2.49)
В справедливости этого равенства опять-таки легко убедиться, проделав выкладки на компонентах.
Теперь сформулируем без доказательства две теоремы. Они очень интересны и весьма полезны для физиков.
В физических задачах часто оказывается, что ротор какой-то величины (скажем, векторного поля А) равен нулю. Мы видели в уравнении (2.46), что ротор градиента равен нулю. (Это легко запоминается по свойствам векторов.) Далее, может оказаться, что Абудет градиентом какой-то величины, потому что тогда ротор Ас необходимостью обратится в нуль. Имеется интересная теорема, утверждающая, что если ротор Аесть нуль, то тогда А непременно окажется чьим - то градиентом; существует некоторое скалярное поле ψ (пси), такое, что A=gradψ. Иными словами, справедлива
ТЕОРЕМА
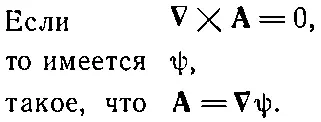 (2.50)
(2.50)
Сходная теорема формулируется и для случая, когда дивергенция Аесть нуль. Из уравнения (2.49) видно, что дивергенция ротора любой величины равна всегда нулю. Если вам случайно встретилось векторное поле D, для которого div D— нуль, то вы имеете право заключить, что Dэто ротор некоторого векторного поля С.
ТЕОРЕМА
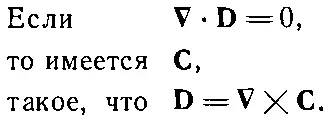 (2.51)
(2.51)
Перебирая всевозможные сочетания двух операторов ∇, мы обнаружили, что два из них всегда дают нуль. Займемся теперь теми, которые не равны нулю. Возьмем комбинацию ∇·( ∇T), первую в нашем списке. В общем случае это не нуль. Выпишем компоненты
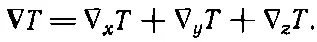
Далее,
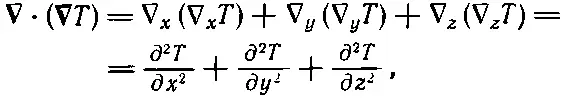 (2.52)
(2.52)
что может, вообще говоря, быть любым числом. Это скалярное поле.
Вы видите, что скобок можно не ставить, а вместо этого писать, не рискуя ошибиться:
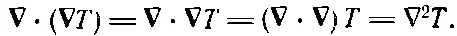 (2.53)
(2.53)
Можно рассматривать ∇ 2как новый оператор. Это скалярный оператор. Так как он в физике встречается часто, ему дали особое имя — лапласиан .
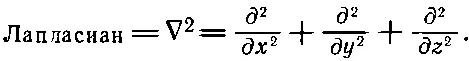 (2.54)
(2.54)
Раз оператор лапласиана —оператор скалярный, он может действовать и на вектор. Под этим мы подразумеваем, что он применяется к каждой компоненте вектора
Читать дальше

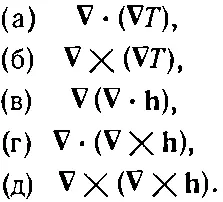 (2.45)
(2.45)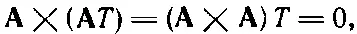
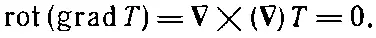 (2.46)
(2.46)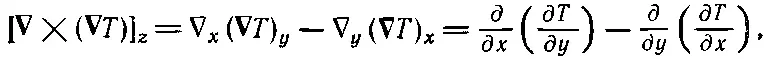 (2.47)
(2.47) (2.48)
(2.48)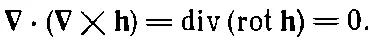 (2.49)
(2.49)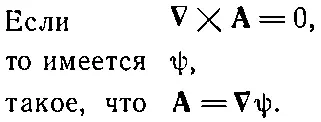 (2.50)
(2.50)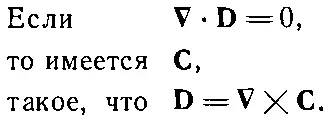 (2.51)
(2.51)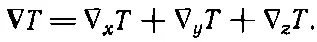
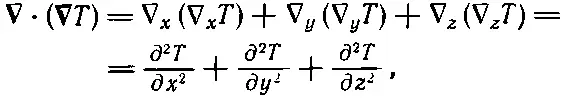 (2.52)
(2.52)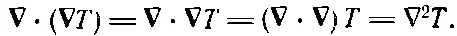 (2.53)
(2.53)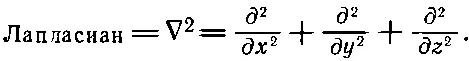 (2.54)
(2.54)



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)


