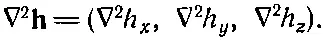
Рассмотрим еще одну возможность: ∇×( ∇× h) [(д) в списке (2.45)]. Ротор от ротора можно написать иначе, если использовать векторное равенство (2.6)
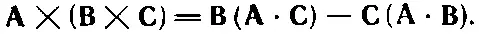 (2.55)
(2.55)
Заменим в этой формуле Аи Воператором ∇и положим C= h. Получится
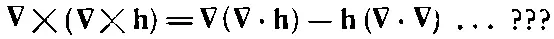
Погодите-ка! Здесь что-то не так. Как и положено, первые два члена — векторы (операторы утолили свою жажду), но последний член совсем не такой. Он все еще оператор. Ошибка в том, что мы не были осторожны и не выдержали нужного порядка членов. Вернувшись обратно, вы увидите, что (2.55) можно с равным успехом записать в виде
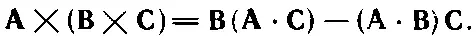 (2.56)
(2.56)
Такой порядок членов выглядит уже лучше. Сделаем нашу подстановку в (2.56). Получится
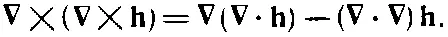 (2.57)
(2.57)
С этой формулой уже все в порядке. Она действительно правильна, в чем вы можете убедиться, расписав компоненты. Последний член — это лапласиан, так что с равным успехом можно написать
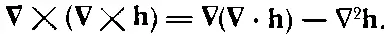 (2.58)
(2.58)
Из нашего списка (2.45) двойных ∇мы разобрали все комбинации, кроме (в), ∇( ∇· h). В ней есть смысл, это — векторное поле, но больше сказать о ней нечего. Это просто векторное поле, которое может случайно возникнуть в каком-нибудь расчете.
Удобно будет все наши рассуждения свести теперь в таблицу:
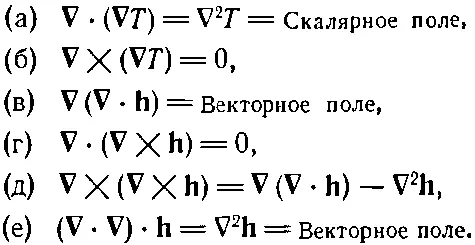 (2.59)
(2.59)
Вы могли заметить, что мы не пытались изобрести новый векторный оператор ∇× ∇. Понимаете, почему?
Мы применили наши знания обычной векторной алгебры к алгебре оператора ∇. Здесь нужно быть осторожным, иначе легко напутать. Нужно упомянуть о двух подвохах (впрочем, в нашем курсе они не встретятся). Что можете вы сказать о следующем выражении, куда входят две скалярные функции ψ и φ (фи):

Вы можете подумать, что это нуль, потому что оно похоже на
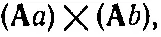
а это всегда равно нулю (векторное произведение двух одинаковых векторов А× Авсегда нуль). Но в нашем примере два оператора ∇отнюдь не одинаковы! Первый действует на одну функцию, ψ, а второй — на другую, φ. И хотя мы изображаем их одним и тем же значком ∇, они все же должны рассматриваться как разные операторы. Направление ∇ψ зависит от функции ψ, а направление ∇φ — от функции φ, так что они не обязаны быть параллельными:
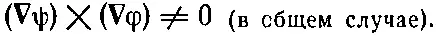
К счастью, к таким выражениям мы прибегать не будем. (Но сказанное нами не меняет того факта, что ∇φ× ∇ψ=0 в любом скалярном поле: здесь обе ∇действуют на одну и ту же функцию.) Подвох номер два (он тоже в нашем курсе не встретится): правила, которые мы здесь наметили, выглядят просто и красиво только в прямоугольных координатах. Например, если мы хотим написать x-компоненту выражения ∇ 2 h, то сразу пишем
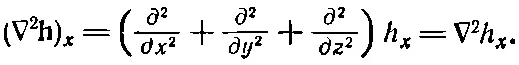 (2.60)
(2.60)
Но это выражение не годится , если мы ищем радиальную компоненту ∇ 2 h. Она не равна ∇ 2h r. Дело в том, что в алгебре векторов все их направления полностью определены. А когда мы имеем дело с векторными полями, то их направления в разных местах различны. Когда мы пробуем описать векторное поле, например, в полярных координатах, то «радиальное» направление меняется от точки к точке. И начав дифференцировать компоненты, вы запросто можете попасть в беду. Даже в постоянном векторном поле радиальная компонента от точки к точке меняется.
Читать дальше

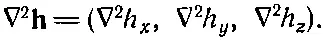
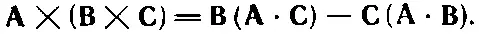 (2.55)
(2.55)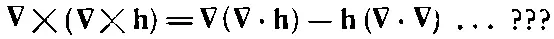
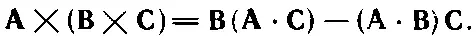 (2.56)
(2.56)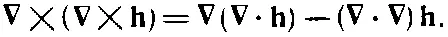 (2.57)
(2.57)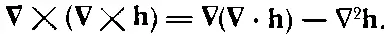 (2.58)
(2.58)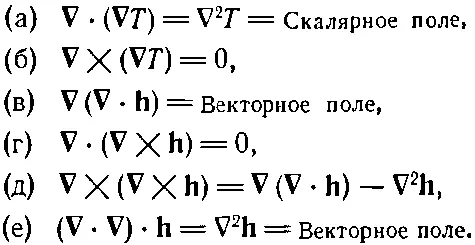 (2.59)
(2.59)
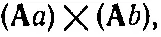
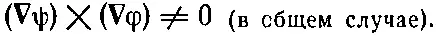
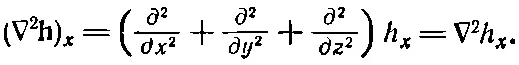 (2.60)
(2.60)



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)


