но нужно помнить, что операторная алгебра немного отличается от обычной векторной. Надо всегда выдерживать правильный порядок операторов, чтобы их операции имели смысл. Тогда у вас трудностей не возникнет, если вы припомните, что оператор ∇подчиняется тем же условиям, что и производные. То, что вы дифференцируете, должно быть поставлено справа от ∇Порядок здесь существен.
Если помнить о порядке, то сразу ясно, что Т ∇— это оператор, а произведение ∇ Т — это уже не «жаждущий» оператор, его жажда утолена. Это физическая величина, имеющая смысл. Он представляет собой скорость пространственного изменения Т : x -компонента ∇ Т показывает, насколько быстро Т изменяется в x-направлении. А куда направлен вектор ∇ Т ? Мы знаем, что скорость изменения Т в каком-то направлении — это компонента ∇ Т в этом направлении [см. (2.15)]. Отсюда следует, что направление ∇ Т — это то, по которому ∇ Т обладает самой длинной проекцией; иными словами, то, по которому ∇ Т меняется быстрее всего. Направление градиента Т — это направление быстрейшего подъема величины Т .
Можно ли с векторным оператором ∇производить другие алгебраические действия? Попробуем скомбинировать его с вектором. Из двух векторов можно составить скалярное произведение, причем двоякого рода:
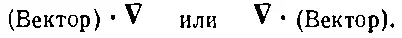
Первое выражение пока что ничего не означает — это все еще оператор. Окончательный смысл его зависит от того, на что он будет действовать. А второе произведение — это некое скалярное поле (потому что А· В— всегда скаляр).
Попробуем составить скалярное произведение ∇на известное поле, скажем на h. Распишем покомпонентно
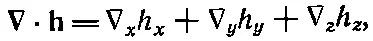 (2.32)
(2.32)
или
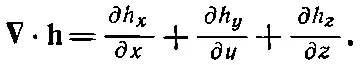 (2.33)
(2.33)
Эта сумма инвариантна относительно преобразования координат. Если выбрать другую систему (отмеченную штрихами), то получилось бы [5] Мы рассматриваем h как физическую величину, зависящую от положения в пространстве, а не как заданную математически функцию трех переменных. Когда h «дифференцируется» по х, у и z или по х', у' и z', то математическое выражение для h должно быть предварительно выражено в виде функции соответствующих переменных. Поэтому в новой системе координат мы не отмечаем h штрихом.
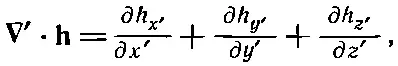 (2.34)
(2.34)
а это — то же самое число, которое получилось бы и из (2.33), хотя с виду оно выглядит иначе, т. е.
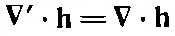 (2.35)
(2.35)
в любой точке пространства. Итак, ∇· h— это скалярное поле, и оно должно представить собой некоторую физическую величину. Вы должны понимать, что комбинация производных в ∇· hимеет довольно специальный вид. Могут быть и другие комбинации всяческого вида, скажем dh y / dx , которые не являются ни скалярами, ни компонентами векторов.
Скалярная величина ∇·(Вектор) очень широко применяется в физике. Ей присвоили имя «дивергенция», или «расходимость». Например,
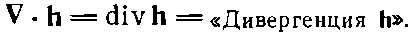 (2.36)
(2.36)
Можно было бы, как и для ∇T, описать физический смысл ∇· h. Но мы отложим это до лучших времен.
Посмотрим сначала, что еще можно испечь из векторного оператора ∇. Как насчет векторного произведения? Можно надеяться, что
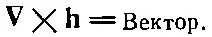 (2.37)
(2.37)
Компоненты этого вектора можно написать, пользуясь обычным правилом для векторного произведения [см. (2.2)]:
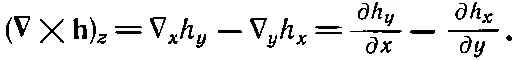 (2.38)
(2.38)
Подобно этому,
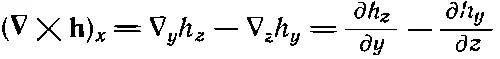 (2.39)
(2.39)
Читать дальше

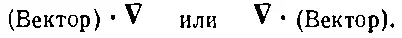
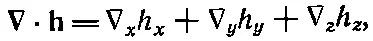 (2.32)
(2.32)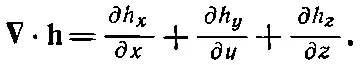 (2.33)
(2.33)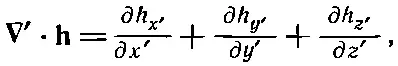 (2.34)
(2.34)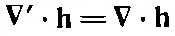 (2.35)
(2.35)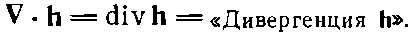 (2.36)
(2.36)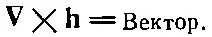 (2.37)
(2.37)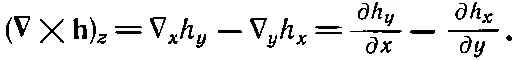 (2.38)
(2.38)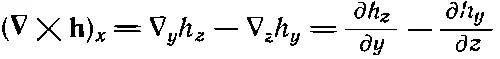 (2.39)
(2.39)



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)


